Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Đây là toán nâng cao chuyên đề giải phương trình nghiệm nguyên, cấu trúc thi chuyên, thi học sinh giỏi các cấp. Hôm nay, Olm sẽ hướng dẫn các em giải chi tiết dạng này bằng lập bảng như sau:
(\(x-5\))(\(x+y-2\)) = 31
31 = 31 ⇒ Ư(31) = {-31; -1; 1; 31}
Lập bảng ta có:
| \(x-5\) | -31 | -1 | 1 | 31 |
| \(x\) | -26 | 4 | 6 | 36 |
| \(x+y-2\) | -1 | -31 | 31 | 1 |
| y | 27 | -33 | 27 | -33 |
Theo bảng trên ta có:
(\(x;y\)) = (-26; 27); (4; -33); (6; 27); (36; - 33)
Vậy (\(x;y\)) = (-26; 27); (4; -33); (6; 27); (36; - 33)

Diện tích hình vuông là 36 cm2
Đề cho sẵn rồi em nhé.

a: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(BC=\sqrt{6^2+8^2}=10\left(cm\right)\)
Xét ΔABC vuông tại A có AH là đường cao
nên \(AH\cdot BC=AB\cdot AC\)
=>\(AH=\dfrac{6\cdot8}{10}=4,8\left(cm\right)\)
Xét ΔABC vuông tại A có \(sinB=\dfrac{AC}{BC}=\dfrac{8}{10}=\dfrac{4}{5}\)
nên \(\widehat{B}\simeq53^0\)
b: Xét ΔABC vuông tại A có \(cosB=\dfrac{BA}{BC};cosC=\dfrac{AC}{BC}\)
\(AB\cdot cosB+AC\cdot cosC\)
\(=AB\cdot\dfrac{AB}{BC}+AC\cdot\dfrac{AC}{BC}\)
\(=\dfrac{AB^2+AC^2}{BC}=\dfrac{BC^2}{BC}=BC\)
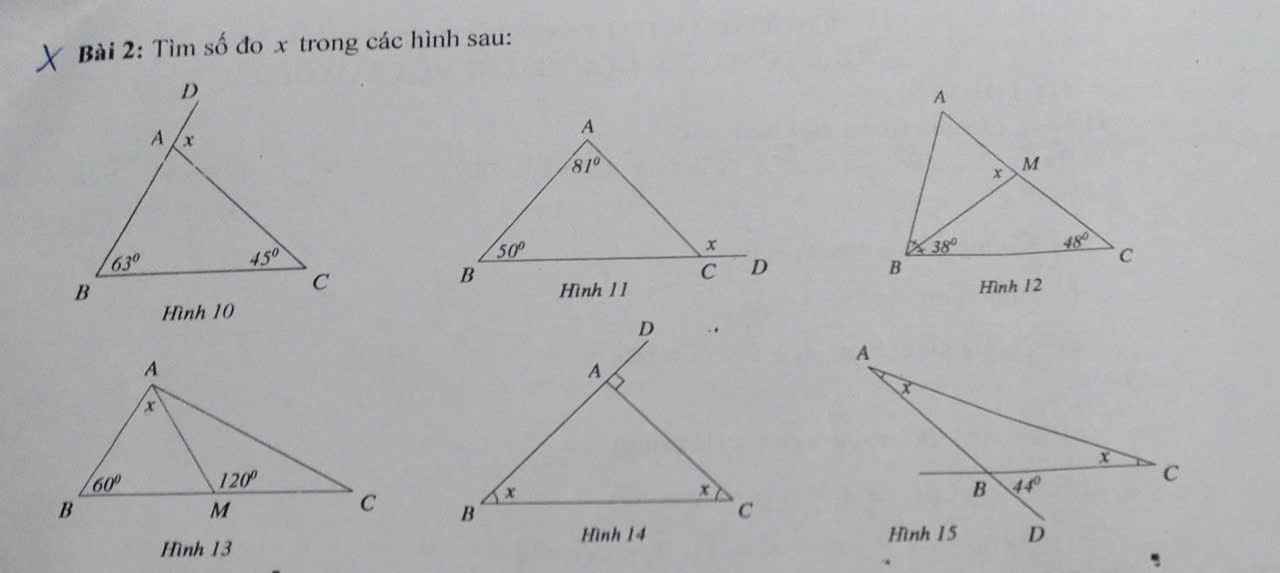
Hình 10: Xét ΔBAC có \(\widehat{CAD}\) là góc ngoài tại đỉnh A
nên \(\widehat{CAD}=\widehat{ABC}+\widehat{ACB}\)
=>\(x=63^0+45^0=108^0\)
Hình 11: Xét ΔABC có \(\widehat{ACD}\) là góc ngoài tại đỉnh C
nên \(\widehat{ACD}=\widehat{CAB}+\widehat{CBA}\)
=>\(x=81^0+50^0=131^0\)
Hình 12: Xét ΔBMC có \(\widehat{AMB}\) là góc ngoài tại đỉnh M
nên \(\widehat{AMB}=\widehat{MBC}+\widehat{MCB}\)
=>\(x=38^0+48^0=86^0\)
Hình 13: Xét ΔMAB có \(\widehat{AMC}\) là góc ngoài tại đỉnh M
nên \(\widehat{AMC}=\widehat{MAB}+\widehat{MBA}\)
=>\(x+60^0=120^0\)
=>\(x=60^0\)
Hình 14: Xét ΔBAC có \(\widehat{CAD}\) là góc ngoài tại đỉnh A
nên \(\widehat{CAD}=\widehat{ABC}+\widehat{ACB}\)
=>\(x+x=90^0\)
=>\(2x=90^0\)
=>\(x=45^0\)
Hình 15:
Xét ΔABC có \(\widehat{CBD}\) là góc ngoài tại đỉnh B
nên \(\widehat{CBD}=\widehat{BAC}+\widehat{BCA}\)
=>\(x+x=44^0\)
=>\(2x=44^0\)
=>\(x=22^0\)