Tìm giá trị lớn nhất, giá trị nhỏ nhất của biểu thức: T= y-2x+4 với 36x2 +16y2 =9
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\dfrac{40404}{70707}-\dfrac{1}{14}\)
\(=\dfrac{4}{7}-\dfrac{1}{14}\)
\(=\dfrac{8}{14}-\dfrac{1}{14}=\dfrac{7}{14}=\dfrac{1}{2}\)

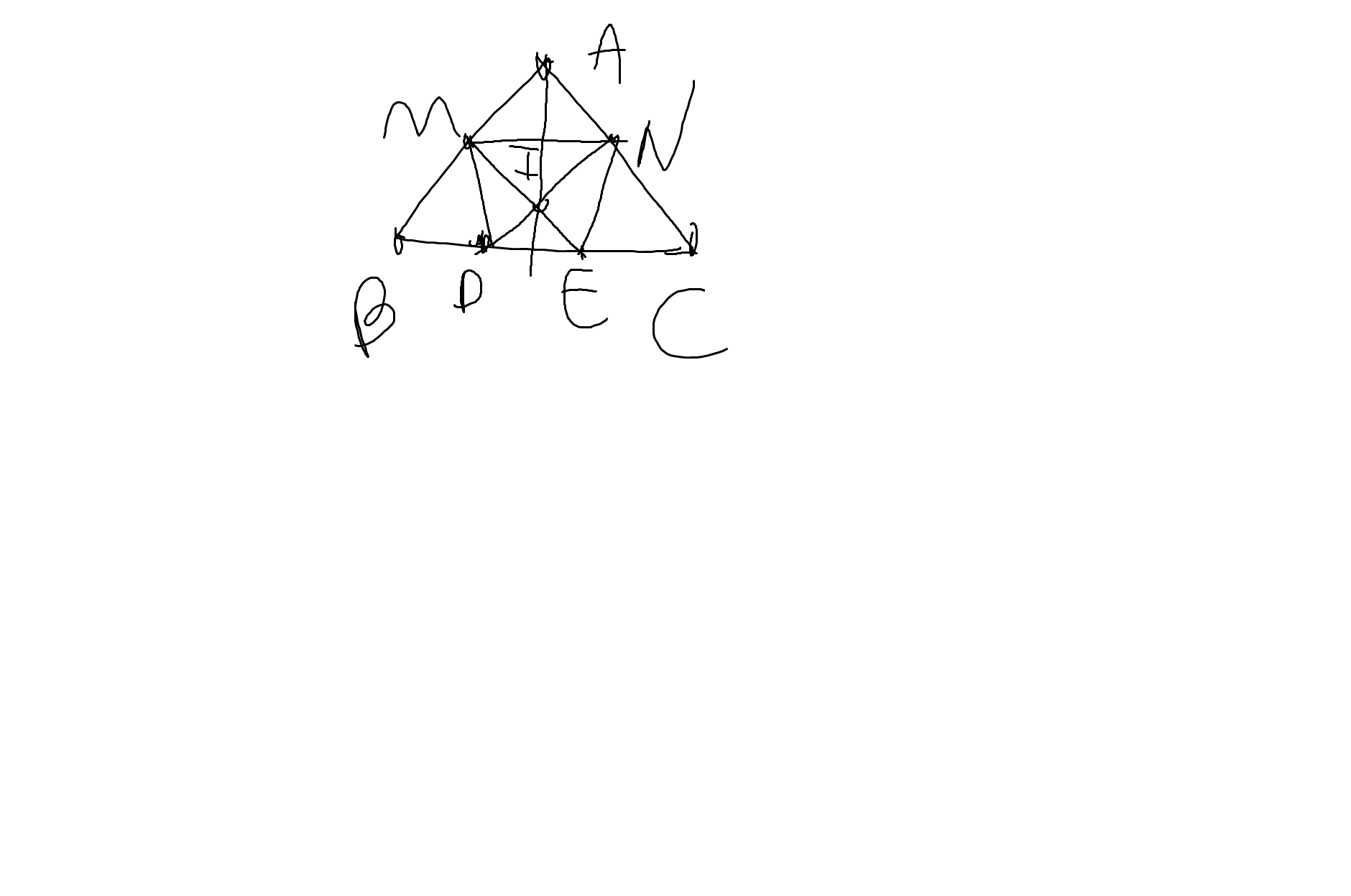
a: BE=BD+DE
CD=CE+DE
mà BD=CE
nên BE=CD
Ta có: \(AM=MB=\dfrac{AB}{2}\)
\(AN=NC=\dfrac{AC}{2}\)
mà AB=AC
nên AM=MB=AN=NC
Xét ΔMBE và ΔNCD có
MB=NC
\(\widehat{MBE}=\widehat{NCD}\)
BE=CD
Do đó: ΔMBE=ΔNCD
=>ME=ND
b:
Xét ΔABC có \(\dfrac{AM}{AB}=\dfrac{AN}{AC}\)
nên MN//BC
=>MN//DE
Xét tứ giác MNED có
MN//ED
ME=ND
Do đó: MNED là hình bình hành
=>MD=NE
Xét ΔMDE và ΔNED có
MD=NE
DE chung
ME=ND
Do đó: ΔMDE=ΔNED
=>\(\widehat{MED}=\widehat{NDE}\)
=>\(\widehat{IDE}=\widehat{IED}\)
=>ΔIED cân tại I
c: Ta có: \(\widehat{IDE}+\widehat{IDB}=180^0\)(hai góc kề bù)
\(\widehat{IED}+\widehat{IEC}=180^0\)(hai góc kề bù)
mà \(\widehat{IDE}=\widehat{IED}\)
nên \(\widehat{IDB}=\widehat{IEC}\)
Xét ΔIDB và ΔIEC có
ID=IE
\(\widehat{IDB}=\widehat{IEC}\)
DB=EC
Do đó: ΔIDB=ΔIEC
=>IB=IC
=>I nằm trên đường trung trực của BC(1)
ta có: AB=AC
=>A nằm trên đường trung trực của BC(2)
Từ (1),(2) suy ra AI là đường trung trực của BC
=>AI\(\perp\)BC

Bài 7:
p là số nguyên tố lớn hơn 3
=>p=3k+1 hoặc p=3k+2
Nếu p=3k+1 thì \(8p+1=8\left(3k+1\right)+1=24k+9=3\left(8k+3\right)⋮3\)
=>Loại
=>p=3k+2
\(4p+1=4\left(3k+2\right)+1=12k+9=3\left(4k+3\right)⋮3\)
=>4p+1 là hợp số
Bài 6:
a: TH1: p=3
p+2=3+2=5; p+4=3+4=7
=>Nhận
TH2: p=3k+1
p+2=3k+1+2=3k+3=3(k+1)
=>Loại
TH3: p=3k+2
p+4=3k+2+4=3k+6=3(k+2)
=>Loại
b: TH1: p=5
p+2=5+2=7; p+6=5+6=11; p+18=5+18=23; p+24=5+24=29
=>Nhận
TH2: p=5k+1
p+24=5k+1+24=5k+25=5(k+5)
=>Loại
TH3: p=5k+2
p+18=5k+2+18=5k+20=5(k+4)
=>Loại
TH4: p=5k+3
p+2=5k+3+2=5k+5=5(k+1)
=>Loại
TH5: p=5k+4
p+6=5k+4+6=5k+10=5(k+2)
=>Loại
Vậy: p=5
Bài 5:
Với p=2 => 7p+5=7*2 + 5 = 19 (tm)
Với p>3
TH1: p=3k+1
=> 7(3k+1)+5=21k+7+5=21k+12=3(7k+4) ⋮ 3
=> 7p+5 là hợp số
TH2: p=3k+2
=>7(3k+2)+5=21k+14+5=21k+19
Vì p là số nguyên tố lớn hơn 3 => p lẻ => 3k + 2 lẻ => 3k lẻ => k lẻ
k lẻ => 21k lẻ => 21k + 19 chẵn => 21k+19 ⋮ 2
=> 7p+5 là hơn số
Vậy có p=2 là thỏa mãn

\(A=100^2-99^2+98^2-97^2+...+2^2-1^2\)
\(=\left(100-99\right)\left(100+99\right)+\left(98-97\right)\left(98+97\right)+...+\left(2-1\right)\left(2+1\right)\)
=100+99+98+97+...+2+1
\(=\dfrac{100\cdot101}{2}=50\cdot101=5050\)
\(A=100^2-99^2+98^2-97^2+...+2^2-1^2\\ =\left(100^2-99^2\right)+\left(98^2-97^2\right)+...+\left(2^2-1^2\right)\\ =\left(100-99\right)\left(100+99\right)+\left(98-97\right)\left(98+97\right)+...+\left(2-1\right)\left(2+1\right)\\ =199+195+...+7+3\\ =\dfrac{\left[\left(199-3\right):4+1\right]\cdot\left(199+3\right)}{2}\\ =\dfrac{\left(196:4+1\right)\cdot202}{2}\\ =5050\)

Tổng số gà trống và gà mái sau khi bán đi là:
128-28-40=100-40=60(con)
Số gà trống sau khi bán đi là 60:2=30(con)
Số gà trống ban đầu là 30+40=70(con)
Số gà mái ban đầu là 128-70=58(con)


Trong 1 giờ, anh quét được: \(\dfrac{1}{4}\)(ngõ)
Trong 1 giờ, em quét được: \(\dfrac{1}{6}\)(ngõ)
Trong 1 giờ, hai anh em quét được: \(\dfrac{1}{4}+\dfrac{1}{6}=\dfrac{3}{12}+\dfrac{2}{12}=\dfrac{5}{12}\)(ngõ)
Thời gian để hai anh em quét xong cái ngõ là:
\(1:\dfrac{5}{12}=\dfrac{12}{5}\left(giờ\right)\)

Số bị trừ lớn số trừ 78 đơn vị
=>Hiệu là 78
Số trừ là 78+8=86
Số bị trừ là 78+86=164

\(\dfrac{21}{25}\times\dfrac{2}{5}+\dfrac{21}{25}\times\dfrac{3}{5}\)
\(=\dfrac{21}{25}\times\left(\dfrac{2}{5}+\dfrac{3}{5}\right)=\dfrac{21}{25}\times\dfrac{5}{5}=\dfrac{21}{25}\)
