K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
5 tháng 7
Bài 2:
1: \(\dfrac{1}{5^{x-1}}+3\cdot5^{2-x}=\dfrac{16}{125}\)
=>\(\dfrac{1}{5^x\cdot\dfrac{1}{5}}+3\cdot\dfrac{25}{5^x}=\dfrac{16}{125}\)
=>\(\dfrac{5}{5^x}+\dfrac{75}{5^x}=\dfrac{16}{125}\)
=>\(\dfrac{80}{5^x}=\dfrac{16}{125}\)
=>\(5^x=80\cdot\dfrac{125}{16}=5\cdot125=5^4\)
=>x=4
2: \(\left(3-\left|x-\dfrac{1}{2}\right|\right)\left(\dfrac{8}{15}-\dfrac{1}{5}\right)+\dfrac{2}{3}=1\)
=>\(\left(3-\left|x-\dfrac{1}{2}\right|\right)\cdot\dfrac{1}{3}=1-\dfrac{2}{3}=\dfrac{1}{3}\)
=>\(3-\left|x-\dfrac{1}{2}\right|=1\)
=>\(\left|x-\dfrac{1}{2}\right|=3-1=2\)
=>\(\left[{}\begin{matrix}x-\dfrac{1}{2}=2\\x-\dfrac{1}{2}=-2\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2+\dfrac{1}{2}=\dfrac{5}{2}\\x=-2+\dfrac{1}{2}=-\dfrac{3}{2}\end{matrix}\right.\)
Bài 3:
1: Gọi ba phần được chia lần lượt là x,y,z
Ba phần tỉ lệ với 2/5;3/4;1/6 nên \(\dfrac{x}{\dfrac{2}{5}}=\dfrac{y}{\dfrac{3}{4}}=\dfrac{z}{\dfrac{1}{6}}\)
=>\(2,5x=\dfrac{4}{3}y=6z\)
=>\(15x=8y=36z\)
=>\(\dfrac{15x}{360}=\dfrac{8y}{360}=\dfrac{36z}{360}\)
=>\(\dfrac{x}{24}=\dfrac{y}{45}=\dfrac{z}{10}=k\)
=>x=24k; y=45k; z=10k
\(x^2+y^2+z^2=24309\)
=>\(\left(24k\right)^2+\left(45k\right)^2+\left(10k\right)^2=24309\)
=>\(k^2=9\)
=>\(\left[{}\begin{matrix}k=3\\k=-3\end{matrix}\right.\)
TH1: k=3
=>\(x=24\cdot3=72;y=45\cdot3=135;z=10\cdot3=30\)
TH2: k=-3
=>\(x=24\cdot\left(-3\right)=-72;y=45\cdot\left(-3\right)=-135;z=10\cdot\left(-3\right)=-30\)
5 tháng 7
a: Xét ΔIAM vuông tại M và ΔIAQ vuông tại Q có
AI chung
\(\widehat{MAI}=\widehat{QAI}\)
Do đó: ΔIAM=ΔIAQ
b: ta có: ΔIAM=ΔIAQ
=>IM=IQ
Xét ΔBMI vuông tại M và ΔBNI vuông tại N có
BI chung
\(\widehat{MBI}=\widehat{NBI}\)
Do đó: ΔBMI=ΔBNI
=>IM=IN
mà IM=IQ
nên IM=IN=IQ
5 tháng 7
a: Xét ΔIAM vuông tại M và ΔIAQ vuông tại Q có
AI chung
\(\widehat{MAI}=\widehat{QAI}\)
Do đó: ΔIAM=ΔIAQ
b: ta có: ΔIAM=ΔIAQ
=>IM=IQ
Xét ΔBMI vuông tại M và ΔBNI vuông tại N có
BI chung
\(\widehat{MBI}=\widehat{NBI}\)
Do đó: ΔBMI=ΔBNI
=>IM=IN
mà IM=IQ
nên IM=IN=IQ
mn giúp e vs ạ
5 tháng 7
Bài 15:
1: \(A=4x-x^2+1\)
\(=-\left(x^2-4x-1\right)\)
\(=-\left(x^2-4x+4-5\right)\)
\(=-\left(x-2\right)^2+5< =5\forall x\)
Dấu '=' xảy ra khi x-2=0
=>x=2
2: \(B=3-4x-x^2\)
\(=-\left(x^2+4x-3\right)\)
\(=-\left(x^2+4x+4-7\right)\)
\(=-\left(x+2\right)^2+7< =7\forall x\)
Dấu '=' xảy ra khi x+2=0
=>x=-2
3: \(C=8-x^2-5x\)
\(=-\left(x^2+5x-8\right)\)
\(=-\left(x^2+2\cdot x\cdot\dfrac{5}{2}+\dfrac{25}{4}-\dfrac{57}{4}\right)\)
\(=-\left(x+\dfrac{5}{2}\right)^2+\dfrac{57}{4}< =\dfrac{57}{4}\forall x\)
Dấu '=' xảy ra khi \(x+\dfrac{5}{2}=0\)
=>\(x=-\dfrac{5}{2}\)
4: \(D=-x^2+6x-4\)
\(=-\left(x^2-6x+4\right)\)
\(=-\left(x^2-6x+9-5\right)\)
\(=-\left(x-3\right)^2+5< =5\forall x\)
Dấu '=' xảy ra khi x-3=0
=>x=3
5: \(E=-10-x^2-6x\)
\(=-\left(x^2+6x+10\right)=-\left(x^2+6x+9+1\right)\)
\(=-\left(x+3\right)^2-1< =-1\forall x\)
Dấu '=' xảy ra khi x+3=0
=>x=-3
6: \(F=-x^2+13x+1\)
\(=-\left(x^2-13x-1\right)\)
\(=-\left(x^2-2\cdot x\cdot\dfrac{13}{2}+\dfrac{169}{4}-\dfrac{173}{4}\right)\)
\(=-\left(x-\dfrac{13}{2}\right)^2+\dfrac{173}{4}\le\dfrac{173}{4}\forall x\)
Dấu '=' xảy ra khi x-13/2=0
=>x=13/2
7: \(G=-4x^2+8x-7\)
\(=-\left(4x^2-8x+7\right)\)
\(=-\left(4x^2-8x+4+3\right)\)
\(=-\left(2x-2\right)^2-3< =-3\forall x\)
Dấu '=' xảy ra khi 2x-2=0
=>2x=2
=>x=1
8: \(H=-4x^2-12x\)
\(=-\left(4x^2+12x\right)\)
\(=-\left(4x^2+12x+9-9\right)\)
\(=-\left(2x+3\right)^2+9< =9\forall x\)
Dấu '=' xảy ra khi 2x+3=0
=>x=-3/2
9: \(I=3x-9x^2-1\)
\(=-9\left(x^2-\dfrac{1}{3}x+\dfrac{1}{9}\right)\)
\(=-9\left(x^2-2\cdot x\cdot\dfrac{1}{6}+\dfrac{1}{36}+\dfrac{1}{12}\right)\)
\(=-9\left(x-\dfrac{1}{6}\right)^2-\dfrac{3}{4}< =-\dfrac{3}{4}\forall x\)
Dấu '=' xảy ra khi x-1/6=0
=>x=1/6
10: \(K=7-9x^2-8x\)
\(=-9\left(x^2+\dfrac{8}{9}x-\dfrac{7}{9}\right)\)
\(=-9\left(x^2+2\cdot x\cdot\dfrac{4}{9}+\dfrac{16}{81}-\dfrac{79}{81}\right)=-9\left(x+\dfrac{4}{9}\right)^2+\dfrac{79}{9}< =\dfrac{79}{9}\forall x\)
Dấu '=' xảy ra khi x+4/9=0
=>x=-4/9
CM
1
T
4 tháng 7
ĐKXĐ: \(x\notin\left\{-1;-4;-6;3\right\}\)
\(\dfrac{3}{x^2+5x+4}+\dfrac{2}{x^2+10x+24}=\dfrac{4}{3}+\dfrac{9}{x^2+3x-18}\\ \Leftrightarrow\dfrac{3}{\left(x+1\right)\left(x+4\right)}+\dfrac{2}{\left(x+4\right)\left(x+6\right)}-\dfrac{9}{\left(x-3\right)\left(x+6\right)}=\dfrac{4}{3}\\ \Leftrightarrow\dfrac{1}{x+1}-\dfrac{1}{x+4}+\dfrac{1}{x+4}-\dfrac{1}{x+6}-\left(\dfrac{1}{x-3}-\dfrac{1}{x+6}\right)=\dfrac{4}{3}\\ \Leftrightarrow\dfrac{1}{x+1}-\dfrac{1}{x-3}=\dfrac{4}{3}\\ \Leftrightarrow\dfrac{x-3-x-1}{\left(x+1\right)\left(x-3\right)}=\dfrac{4}{3}\\ \Rightarrow4\left(x^2-2x-3\right)=3.\left(-4\right)\\ \Leftrightarrow4x^2-8x-12=-12\\ \Leftrightarrow4x\left(x-2\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x-2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\left(tm\right)\\x=2\left(tm\right)\end{matrix}\right.\)
4 tháng 7
\(\left(1^3+2^3+3^3+4^3+5^3+6^3+7^3+8^3+9^3+10^3\right)\)
\(=\left(1+2+3+...+10\right)^2\)
\(=\left(\dfrac{10\cdot11}{2}\right)^2=\left(5\cdot11\right)^2=25\cdot121⋮11\)
4 tháng 7
Ta sẽ chứng minh \(1^3+2^3+3^3+...+n^3=\left[\dfrac{n\left(n+1\right)}{2}\right]^2\) bằng quy nạp. (*)
Thật vậy, với \(n=1\) thì (*) thành \(1^3=\left[\dfrac{1.2}{2}\right]^2\), luôn đúng
Giả sử (*) đúng đến \(n=k\ge1\), khi đó cần chứng minh (*) đúng với \(n=k+1\). Thật vậy, với \(n=k+1\) thì
\(VT=1^3+2^3+3^2+...+k^3+\left(k+1\right)^3\)
\(=\left[\dfrac{k\left(k+1\right)}{2}\right]^2+\left(k+1\right)^3\) (theo giả thiết quy nạp)
\(=\left(k+1\right)^2\left(\dfrac{k^2}{4}+k+1\right)\)
\(=\left(k+1\right)^2\left(\dfrac{k^2+4k+4}{4}\right)\)
\(=\dfrac{\left(k+1\right)^2\left(k+2\right)^2}{4}\)
\(=\left[\dfrac{\left(k+1\right)\left(k+2\right)}{2}\right]^2\)
Vậy (*) đúng với \(n=k+1\). Theo nguyên lí quy nạp, (*) được chứng minh.
Như vậy \(1^3+2^3+3^3+...+10^3=\left(\dfrac{10.11}{2}\right)^2=\left(5.11\right)^2=25.11^2⋮11\), ta có đpcm.
4 tháng 7
Gọi mẫu số là x
(ĐIều kiện: \(x\ne0\))
Vì phân số nhỏ hơn 1 nên mẫu số>tử số
=>Mẫu số>32/2=16
Tử số là 32-x
Mẫu số khi tăng thêm 10 đơn vị là x+10
Tử số khi giảm đi một nửa là \(\dfrac{32-x}{2}\)
Phân số mới là 2/17 nên \(\dfrac{32-x}{2}:\left(x+10\right)=\dfrac{2}{17}\)
=>\(\dfrac{32-x}{2x+20}=\dfrac{2}{17}\)
=>17(32-x)=2(2x+20)
=>544-17x=4x+40
=>-21x=40-544=-504
=>x=24
Tử số là 32-24=8
Vậy: Phân số cần tìm là \(\dfrac{8}{24}\)
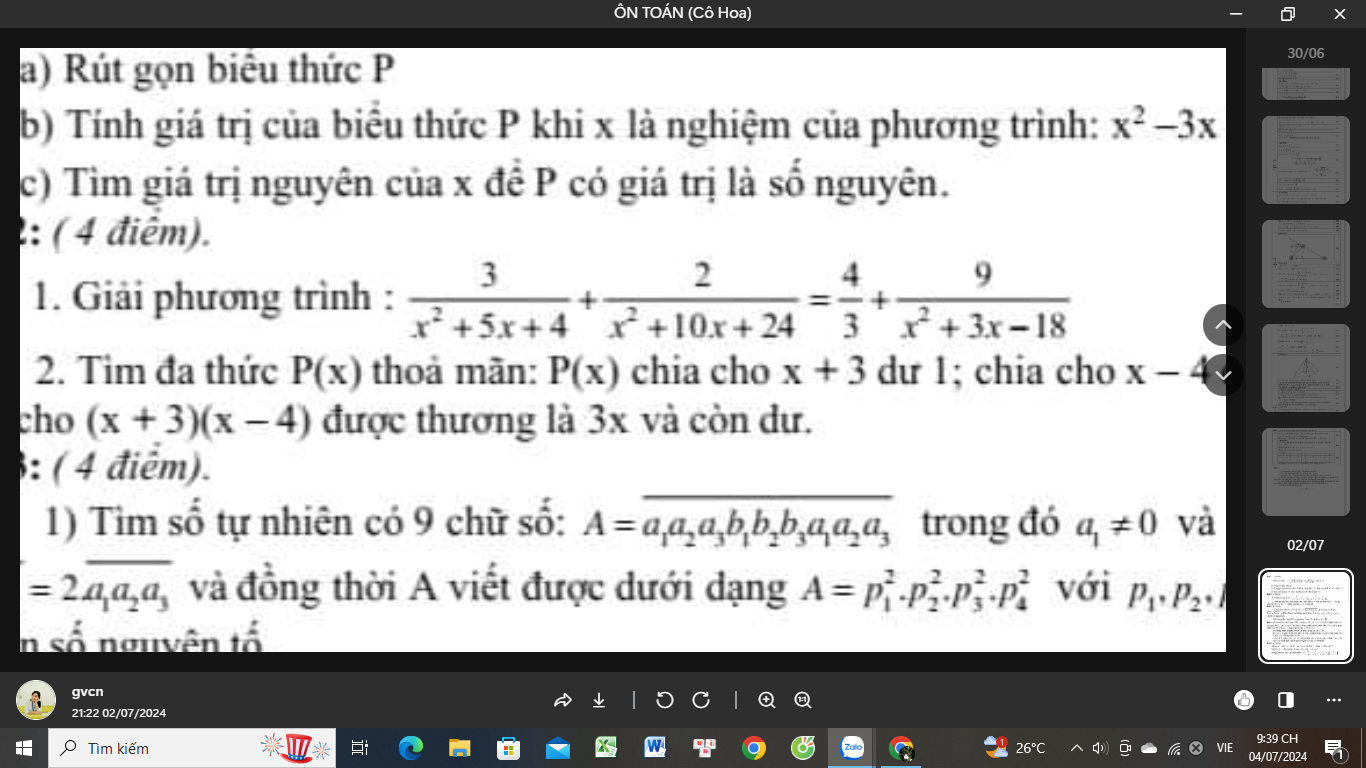
Bài 5:
Áp dụng BĐT Cô si cho 2 số: \(\sqrt{\dfrac{b+c}{a}}\) và 1
Có:
\(\sqrt{\dfrac{b+c}{a}}.1\le\dfrac{\left(\dfrac{b+c}{a}+1\right)}{2}\)
\(\Rightarrow\sqrt{\dfrac{b+c}{a}}\le\dfrac{a+b+c}{2a}\)
\(\Rightarrow\sqrt{\dfrac{a}{b+c}}\ge\dfrac{2a}{a+b+c}\)
Tương tự: \(\sqrt{\dfrac{b}{a+c}}\ge\dfrac{2b}{a+b+c}\)
\(\sqrt{\dfrac{c}{a+b}}\ge\dfrac{2c}{a+b+c}\)
\(\Rightarrow\sqrt{\dfrac{a}{b+c}}+\sqrt{\dfrac{b}{a+c}}+\sqrt{\dfrac{c}{a+b}}\ge\dfrac{2a}{a+b+c}+\dfrac{2b}{a+b+c}+\dfrac{2c}{a+b+c}\Rightarrow VT\ge2\Rightarrow VT>1\)