Help me
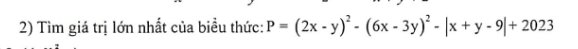
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a,b: Xét ΔMBA và ΔMCD có
MB=MC
\(\widehat{BMA}=\widehat{CMD}\)(hai góc đối đỉnh)
MA=MD
Do đó: ΔMBA=ΔMCD
=>AB=CD
mà AB<AC
nên CD<AC
c: ΔMBA=ΔMCD
=>\(\widehat{MAB}=\widehat{MDC}\left(1\right)\)
Xét ΔCDA có CD<CA
mà \(\widehat{CAD};\widehat{CDA}\) lần lượt là góc đối diện của các cạnh CD,CA
nên \(\widehat{CAD}< \widehat{CDA}\)(2)
Từ (1),(2) suy ra \(\widehat{CAD}< \widehat{MAB}\)

2x³ - 5x² + 8x - 3
= 2x³ - x² - 4x² + 2x + 6x - 3
= (2x³ - x²) - (4x² - 2x) + (6x - 3)
= x²(2x - 1) - 2x(2x - 1) + 3(2x - 1)
= (2x - 1)(x² - 2x + 3)

Do là bài tập cũng gọi là dành cho chuyên hơi khó xíu bt học thêm ấy chỗ ẫy cũng khó nên bài tập ít nhưng mà nâng cao

Gọi x (km/h) là vận tốc của ô tô 1 (x > 10)
Vận tốc của ô tô 2 là: x - 10 (km/h)
Thời gian ô tô 1 đi từ A đến B:
 Thời gian ô tô 2 đi từ A đến B:
Thời gian ô tô 2 đi từ A đến B:
 Theo đề bài, ta có phương trình:
Theo đề bài, ta có phương trình:
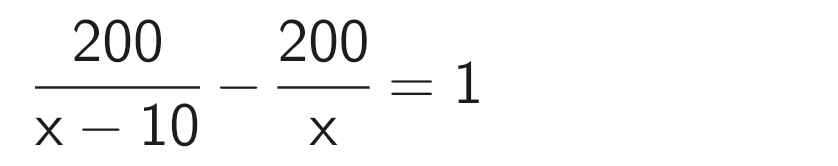 200x - 200(x - 10) = x(x - 10)
200x - 200(x - 10) = x(x - 10)
200x - 200x + 2000 = x² - 10x
x² - 10x - 2000 = 0
x² - 50x + 40x - 2000 = 0
(x² - 50x) + (40x - 2000) = 0
x(x - 50) + 40(x - 50) = 0
(x - 50)(x + 40) = 0
x - 50 = 0 hoặc x + 40 = 0
*) x - 50 = 0
x = 50 (nhận)
*) x + 40 = 0
x = -40 (loại)
Vậy vận tốc của xe ô tô 1 là 50 km/h, vận tốc của xe ô tô 2 là 50 - 10 = 40 km/h

a: \(\left(\dfrac{1}{2}x^5-3x^2\right):x^2-x\left(\dfrac{1}{2}x^2+5\right)+2x\left(x-2\right)\left(x+2\right)-\left(x^3-27\right):\left(x-3\right)\)
\(=\dfrac{1}{2}x^3-3-\dfrac{1}{2}x^3-5x+2x\left(x^2-4\right)-\dfrac{\left(x-3\right)\left(x^2+3x+9\right)}{x-3}\)
\(=-5x-3+2x^3-8x-x^2-3x-9\)
\(=2x^3-x^2-16x-12\)
b: \(\left(7x^3-2x^2\right):\left(-2x^2\right)+\left(\dfrac{5}{4}x^2-3x\right):x-\dfrac{1}{2}x\left(x-1\right)\left(2x+1\right)\)
\(=\dfrac{-7}{2}x+1+\dfrac{5}{4}x-3-\dfrac{1}{2}x\left(2x^2+x-2x-1\right)\)
\(=-\dfrac{9}{4}x-2-\dfrac{1}{2}x\left(2x^2-x-1\right)\)
\(=-\dfrac{9}{4}x-2-x^3+\dfrac{1}{2}x^2+\dfrac{1}{2}x\)
\(=-x^3+\dfrac{1}{2}x^2-\dfrac{7}{4}x-2\)

\(x^2-3x+9=-xy+2y\)
\(\Rightarrow x^2-3x+xy-2y=-9\)
\(\Rightarrow\left(x^2+xy\right)-\left(2x+2y\right)-x=-9\)
\(\Rightarrow x\left(x+y\right)-2\left(x+y\right)-x=-9\)
\(\Rightarrow\left(x-2\right)\left(x+y\right)-x=-9\)
\(\Rightarrow\left(x-2\right)\left(x+y\right)-\left(x-2\right)=-7\)
\(\Rightarrow\left(x-2\right)\left(x+y-1\right)=-7\) (1)
Vì x và y nguyên nên (x-2) và (x+y-1) cũng nguyên (2)
Từ (1) và (2) suy ra:
\(\left(x-2\right);\left(x+y-1\right)\inƯ\left(-7\right)=\left\{\text{±}1;\text{±}7\right\}\)
Sau đó thì bạn lập bảng và kết luận nhé!

\(6x^4+7x^3-37x^2-8x+12\\ =6x^4-3x^3+10x^3-5x^2-32x^2+16x-24x+12\\ =3x^3\left(2x-1\right)+5x^2\left(2x-1\right)-16x\left(2x-1\right)-12\left(2x-1\right)\\ =\left(2x-1\right)\left(3x^3+5x^2-16x-12\right)\\ =\left(2x-1\right)\left(3x^3-6x^2+11x^2-22x+6x-12\right)\\ =\left(2x-1\right)\left[3x^2\left(x-2\right)+11x\left(x-2\right)+6\left(x-2\right)\right]\\ =\left(2x-1\right)\left(x-2\right)\left(3x^2+11x+6\right)\\ =\left(2x-1\right)\left(x-2\right)\left(3x^2+9x+2x+6\right)\\ =\left(2x-1\right)\left(x-2\right)\left[3x\left(x+3\right)+2\left(x+3\right)\right]\\ =\left(2x-1\right)\left(x-2\right)\left(x+3\right)\left(3x+2\right)\)

\(x^4+x^3+2x^2+x+1\\= x^4+x^3+x^2+x^2+x+1\\ =x^2\left(x^2+x+1\right)+\left(x^2+x+1\right)\\ =\left(x^2+1\right)\left(x^2+x+1\right)\)
\(P=\left(2x-y\right)^2-\left(6x-3y\right)^2-\left|x+y-9\right|+2023\)
\(=\left(2x-y\right)^2-9\left(2x-y\right)^2-\left|x+y-9\right|+2023\)
\(=-8\left(2x-y\right)^2-\left|x+y-9\right|+2023< =2023\forall x,y\)
Dấu '=' xảy ra khi \(\left\{{}\begin{matrix}2x-y=0\\x+y-9=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=2x\\x+y=9\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=6\\x=3\end{matrix}\right.\)