 bài 1
bài 1
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có:
\(f\left(a\right)+f\left(b\right)=f\left(a\right)+f\left(1-a\right)\\ =\dfrac{100^a}{100^a+10}+\dfrac{100^{1-a}}{100^{1-a}+10}\\ =\dfrac{100^a}{100^a+10}+\dfrac{\dfrac{100}{100^a}}{\dfrac{100}{100^a}+10}\\ =\dfrac{100^a}{100^a+10}+\dfrac{100}{100^a}.\dfrac{100^a}{100+10.100^a}\\ =\dfrac{100^a}{100^a+10}+\dfrac{10}{10+100^a}\\ =\dfrac{100^a+10}{10+100^a}=1\left(đpcm\right)\)

a) Xét có mà suy ra
b) Xét tam giác và .
có là cạnh chung
.
là phân giác của
c) là giao điểm của hai đường cao trong tam giác nên vuông góc với .
Tam giác cân tại có là đường cao nên là đường trung tuyến. Do đó là trung điểm của .
a) Xét có mà suy ra
b) Xét tam giác và .
có là cạnh chung
.
là phân giác của
c) là giao điểm của hai đường cao trong tam giác nên vuông góc với .
Tam giác cân tại có là đường cao nên là đường trung tuyến. Do đó là trung điểm của .

Tổng số cách chọn ra một bạn để phỏng vấn là: 1+5 = 6
Xác suất biến cố bạn nam được chọn là:
\(\left(1:6\right)=\dfrac{1}{6}\approx16,66\%\)
Đs...
Tổng số cách chọn ra một bạn để phỏng vấn là: 1+5 = 6
Xác suất biến cố bạn nam được chọn là:

a) Ta có:
A(x) + B(x) = (2x3 - x2 + 3x - 5) + (2x3 + x2 + x + 5)
= 4x3 + 4x
b) Ta có H(x) = A(x) + B(x) = 4x3 + 4x = 0
=> 4x(x2 + 1) = 0
=> 4x = 0 hoặc x2 + 1 = 0
=> x = 0 : 4 = 0 hoặc x2 = 0 - 1 = -1 (vô lí)
Vậy nghiệm của H(x) = A(x) + B(x) là x = 0

Gọi số sách 2 lớp 7A và 7B lần lượt là a và b ( sách, a,b thuộc N*)
Ta có a + b = 121
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
a/5 = b/6 = a+b/ 5+6 = 121/11 = 11
Quyển sách lớp 7A quyên góp được là:
11 x 5 = 55
Số sách 7B quyên góp được là
11 x 6 = 66
Theo đề bài:
+) Lớp 7A và 7B quyên góp được quyển sách
Nên ta có:
+) Số sách giáo khoa của lớp 6A; lớp 6B tỉ lệ thuận với tỉ lệ thuận với 5; 6
Nên ta có:
Áp dụng tính chất dãy tỉ số bằng nhau ta có
Suy ra: x=55, y= 66 ( thỏa mãn).
Vậy lớp 6A quyên góp được quyển sách, lớp 6B quyên góp được cuốn.

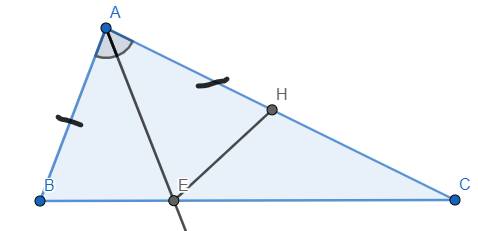
a) Xét ΔABE & ΔAHE có:
- AB = AH (giả thuyết); AE là cạnh chung; \(\widehat{BAE}=\widehat{HAE}\) (vì AE là tia phân giác góc BAC)
Suy ra ΔABE = ΔAHE (c.g.c)
