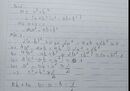Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


b/ B=(cosa−sina)2+(cosa+sina)2+cos4a−sin4a−2cos2aB=(cosa−sina)2+(cosa+sina)2+cos4a−sin4a−2cos2a
=cos2a−2cosa.sina+sin2a+cos2a+2cosa.sina+sin2a+(cos2a+sin2a)(cos2a−sin2a)−2cos2a=cos2a−2cosa.sina+sin2a+cos2a+2cosa.sina+sin2a+(cos2a+sin2a)(cos2a−sin2a)−2cos2a
=2+(cos2a−sin2a)−2cos2a=2+(cos2a−sin2a)−2cos2a
=2−sin2a−cos2a=2−1=1


\(a+b+\frac{4}{a}+\frac{1}{4b}=\frac{25}{36}a+\frac{4}{a}+\frac{25}{36}b+\frac{1}{4b}+\frac{11}{36}\left(a+b\right)\)
\(\ge2\sqrt{\frac{25}{36}a.\frac{4}{a}}+2\sqrt{\frac{25}{36}b.\frac{1}{4b}}+\frac{11}{36}.3\)
\(=\frac{10}{3}+\frac{5}{6}+\frac{11}{12}=\frac{61}{12}\)
Dấu \(=\)khi \(\hept{\begin{cases}\frac{25}{36}a=\frac{4}{a}\\\frac{25}{36}b=\frac{1}{4b}\\a+b=3\end{cases}}\Leftrightarrow\hept{\begin{cases}a=\frac{12}{5}\\b=\frac{3}{5}\end{cases}}\).