\(5x=3y\Rightarrow x=\dfrac{3y}{5}\)

Thay \(x=\dfrac{3y}{5}\) vào biểu thức \(x^2-y^2=-4\) ta có:

\(\left(\dfrac{3y}{5}\right)^2-y^2=-4\)

\(\dfrac{9y^2}{25}-y^2=-4\)

\(-\dfrac{16}{25}y^2=-4\)

\(y^2=-\dfrac{4}{\dfrac{-16}{25}}\)

\(y^2=\dfrac{25}{4}\)

\(\Rightarrow y=-\dfrac{5}{2};y=\dfrac{5}{2}\)

*) \(y=-\dfrac{5}{2}\Rightarrow x=\dfrac{3.\left(-\dfrac{5}{2}\right)}{5}=-\dfrac{3}{2}\)

*) \(y=\dfrac{5}{2}\Rightarrow x=\dfrac{3.\dfrac{5}{2}}{5}=\dfrac{3}{2}\)

Vậy ta được các cặp giá trị \(\left(x;y\right)\) thỏa mãn:

\(\left(-\dfrac{3}{2};-\dfrac{5}{2}\right);\left(\dfrac{3}{2};\dfrac{5}{2}\right)\)

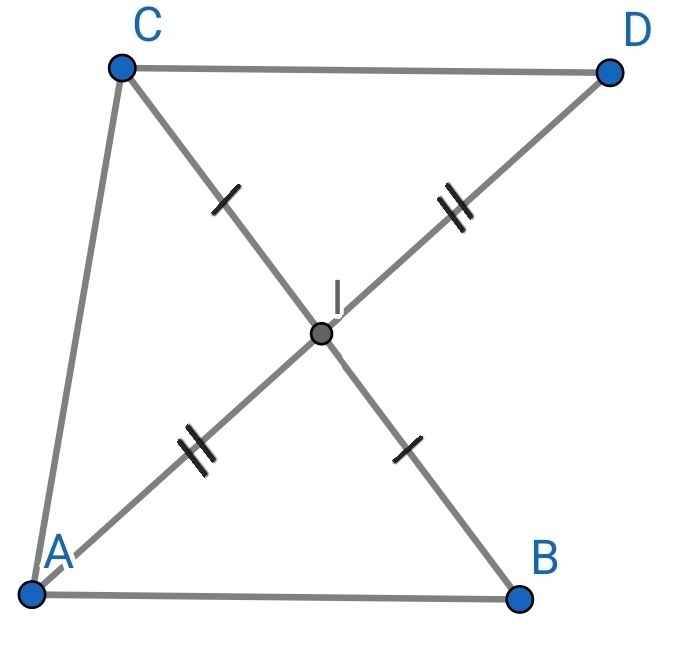 a) Xét ∆CDI và ∆BAI có:

CI = BI (do I là trung điểm của BC)

∠CID = ∠BIA (đối đỉnh)

ID = IA (gt)

⇒ ∆CDI = ∆BAI (c-g-c)

⇒ CD = AB (hai cạnh tương ứng)

b) Do CD = AB (cmt)

Mà AB < AC (gt)

⇒ AC > CD

∆ACD có:

AC > CD (cmt)

⇒ ∠ADC > ∠CAD (quan hệ giữa góc và cạnh đối diện trong tam giác)

⇒ ∠IDC > ∠CAI

Do ∆CDI = ∆BAI (cmt)

⇒ ∠IDC = ∠BAI (hai góc tương ứng)

Mà ∠IDC > ∠CAI

⇒ ∠BAI > ∠CAI

nhanh giúp mình mình hứa sẽ vốt đủ

vote j ạ? ở đây thì bấm đúng bn ạ!

Nói thêm là mik cũng đang cố gắng để đc làm CTV nè!

mình cũng ko hiểu CTVVIP là gì

106

   1 + 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 + 11 + 12 + 13 + 14

= 1 + (14 + 1) x 14 : 2

= 1 + 15 x 14 : 2

= 1 + 15 x 7

= 1 + 105

= 106 

D. Cả A, B, C đều đúng 

    \(\widehat{A}\) : \(\widehat{B}\): \(\widehat{C}\) = 3 : 5 : 7

          \(\dfrac{\widehat{A}}{3}\) = \(\dfrac{\widehat{B}}{5}\) = \(\dfrac{\widehat{C}}{7}\)

Áp dụng tính chất dãy tỉ số bằng nhau ta có:

  \(\dfrac{\widehat{A}}{3}\) = \(\dfrac{\widehat{B}}{5}\) = \(\dfrac{\widehat{C}}{7}\) = \(\dfrac{\widehat{A}+\widehat{B}+\widehat{C}}{3+5+7}\) = \(\dfrac{180^0}{15}\) = `12⁰

   \(\widehat{A}\) = 12⁰ \(\times\) 3  = 36⁰

   \(\widehat{B}\) = 12⁰ \(\times\) 5 = 60⁰ 

   \(\widehat{C}\) = 12⁰ \(\times\) 7 = 84⁰

    Vì 36⁰ < 60⁰ < 84⁰

Vậy \(\widehat{A}\) < \(\widehat{B}\) < \(\widehat{C}\) nên BC < AC < AB (do trong tam giác cạnh đối diện với góc lớn hơn thì lớn hơn và ngược lại)

a/ Xét tg AMB và tg NMC có

MB=MC (gt)

MA=MN (gt)

\(\widehat{AMB}=\widehat{NMC}\) (góc đối đỉnh)

=> tg AMB = tg NMC (c.g.c)

b/

Ta có

tg AMB = tg NMC (cmt) \(\Rightarrow\widehat{ABC}=\widehat{BCN}\) Hai góc trên ở vị trí sole trong

=> AB//CN

\(\Rightarrow\widehat{ADC}=\widehat{DCN}\) (góc so le trong) mà \(\widehat{ADC}=90^o\)

\(\Rightarrow\widehat{DCN}=90^o\)