
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đề thi đánh giá năng lực

\(x=3y\) và y = 5\(x\) thay y = 5\(x\) vào \(x\) = 3y ta có: \(x\) = 3.5\(x\)
⇒ \(x\) = 15\(x\) ⇒ \(x-15x\) = 0 ⇒ \(-14\)\(x\) = 0 ⇒ \(x=0\)
Thay \(x\) = 0 vào y = 5\(x\) ta được: y= 5.0 = 0
Vậy \(x=3\)y; y = 5\(x\) thì y = 0

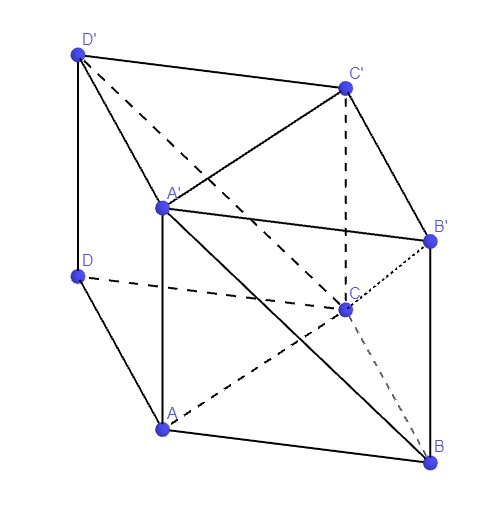
Gọi độ dài cạnh lăng trụ là a
Trong mp (ABC), lấy D đối xứng B qua AC \(\Rightarrow ABCD\) là hình thoi
Trong mp (A'B'C') lấy D' đối xứng B' qua A'C' \(\Rightarrow A'B'C'D'\) là hình thoi
\(\Rightarrow A'BCD'\) là hình bình hành nên \(A'B||D'C\)
\(\Rightarrow\left(A'B,B'C\right)=\left(D'C,B'C\right)=\widehat{B'CD'}\) (nếu nó nhọn, và bằng góc bù với nó nếu nó tù)
\(D'C=A'B=\sqrt{A'A^2+AB^2}=a\sqrt{2}\)
\(B'C=\sqrt{B'B^2+BC^2}=a\sqrt{2}\)
\(B'D'=BD=2.\dfrac{a\sqrt{3}}{2}=a\sqrt{3}\)
Áp dụng định lý hàm cos:
\(cos\widehat{B'CD'}=\dfrac{B'C^2+D'C^2-B'D'^2}{2B'C.D'C}=\dfrac{1}{4}\)
\(\Rightarrow\left(A'B,B'C\right)\approx75^031'\)

Nếu \(f\left(x\right)=0\) có nghiệm trên \(\left[-1;1\right]\Rightarrow\min\limits_{\left[-1;1\right]}\left[f\left(x\right)\right]^2=0\) ko thỏa mãn yêu cầu
\(\Rightarrow f\left(x\right)=0\) vô nghiệm trên \(\left[-1;1\right]\)
Khi đó
\(f'\left(x\right)=3x^2-3=0\Rightarrow\left[{}\begin{matrix}x=-1\\x=1\end{matrix}\right.\)
\(\Rightarrow f'\left(x\right)\le0;\forall x\in\left[-1;1\right]\)
Xét hàm \(y=\left[f\left(x\right)\right]^2\) trên \(\left[-1;1\right]\)
\(y=\left[f\left(x\right)\right]^2\Rightarrow y'=2f'\left(x\right).f\left(x\right)\)
Do \(f'\left(x\right)\le0\) và \(f\left(x\right)=0\) vô nghiệm (nên ko đổi dấu) trên \(\left[-1;1\right]\) nên:
TH1: \(f\left(x\right)>0;\forall x\in\left[-1;1\right]\Rightarrow x^3-3x+1>-m\)
\(\Rightarrow-m< \min\limits_{\left[-1;1\right]}\left(x^3-3x+1\right)=-1\)
\(\Rightarrow m>1\)
Khi đó \(f'\left(x\right).f\left(x\right)\le0\Rightarrow y=\left[f\left(x\right)\right]^2\) nghịch biến trên \(\left[-1;1\right]\)
\(\Rightarrow y_{min}=y\left(1\right)=\left(1-3+m+1\right)^2=\left(m-1\right)^2=1\)
\(\Rightarrow\left[{}\begin{matrix}m=0< 1\left(loại\right)\\m=2\end{matrix}\right.\)
TH2: \(f\left(x\right)< 0;\forall x\in\left[-1;1\right]\Rightarrow x^3-3x+1< -m\)
\(\Rightarrow-m>\max\limits_{\left[-1;1\right]}\left(x^3-3x+1\right)=3\)
\(\Rightarrow m< -3\)
Khi đó \(f'\left(x\right).f\left(x\right)\ge0\Rightarrow y=\left[f\left(x\right)\right]^2\) đồng biến trên \(\left[-1;1\right]\)
\(\Rightarrow y_{min}=y\left(-1\right)=\left(-1+3+m+1\right)^2=\left(m+3\right)^2=1\)
\(\Rightarrow\left[{}\begin{matrix}m=-2>-3\left(loại\right)\\m=-4\end{matrix}\right.\)
Vậy \(m=2;m=-4\) (C đúng)

Không gian mẫu: \(C_{14}^2\)
a. Số cách rút ra 2 bi đỏ: \(C_6^2\)
Xác suất: \(\dfrac{C_6^2}{C_{14}^2}=\dfrac{15}{91}\)
b. Số cách rút 2 viên không có viên xanh nào (nghĩa là 2 viên thuộc 10 viên đỏ hoặc trắng): \(C_{10}^2\) cách
\(\Rightarrow C_{14}^2-C_{10}^2\) cách rút ra ít nhất 1 viên trắng
Xác suất: \(\dfrac{C_{14}^2-C_{10}^2}{C_{14}^2}=\dfrac{46}{91}\)
c. Có 2 trường hợp: bi thứ nhất màu trắng và bi thứ nhất không phải màu trắng.
Xác suất: \(\dfrac{C_4^2}{C_{14}^2}+\dfrac{C_{10}^1}{C_{14}^1}.\dfrac{C_4^1}{C_{13}^1}=\dfrac{2}{7}\)

\(-x^3+3x-7+2m=0\)
\(\Leftrightarrow x^3-3x+7=2m\)
Xét hàm: \(f\left(x\right)=x^3-3x+7\)
\(f'\left(x\right)=3x^2-3=0\Rightarrow x=\pm1\)
Bảng biến thiên:
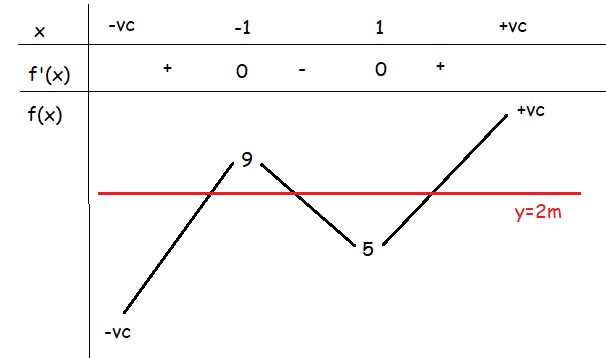
Từ BBT ta thấy pt có 3 nghiệm pb hay \(y=2m\) cắt \(y=f\left(x\right)\) tại 3 điểm pb
\(\Leftrightarrow5< 2m< 9\Rightarrow\dfrac{5}{2}< m< \dfrac{9}{2}\)

Gọi \(A_1\) là biến cố: "2 sản phẩm lấy nhầm từ lô 1 đều là sản phẩm tốt"
\(A_2\) là biến cố: "2 sản phẩm lấy nhầm từ lô 1 có 1 sản phẩm tốt 1 sản phẩm xấu"
`A_3` là biến cố: "2 sản phẩm lấy nhầm từ lô 1 đều là sản phẩm xấu"
\(\Rightarrow P\left(A_1\right)=\dfrac{C_6^2}{C_9^2}=\dfrac{5}{12}\); \(P\left(A_2\right)=\dfrac{C_6^1.C_3^1}{C_9^2}=\dfrac{1}{2}\); \(P\left(A_3\right)=\dfrac{C_3^2}{C_9^2}=\dfrac{1}{12}\)
\(A_1;A_2;A_3\) tạo thành 1 nhóm biến cố đầy đủ
Gọi B là biến cố: "sản phẩm cuối cùng lấy ra là sản phẩm tốt"
\(\Rightarrow P\left(B|A_1\right)=\dfrac{5+2}{7+2}=\dfrac{7}{9}\);
\(P\left(B|A_2\right)=\dfrac{5+1}{7+2}=\dfrac{2}{3}\);
\(P\left(B|A_3\right)=\dfrac{5}{7+2}=\dfrac{5}{9}\)
a.
\(P\left(B\right)=P\left(A_1\right).P\left(B|A_1\right)+P\left(A_2\right).P\left(B|A_2\right)+P\left(A_3\right).P\left(B|A_3\right)\)
\(=\dfrac{5}{12}.\dfrac{7}{9}+\dfrac{1}{2}.\dfrac{2}{3}+\dfrac{1}{12}.\dfrac{5}{9}=\dfrac{19}{27}\)
b.
Gọi `C_1` là biến cố "sản phẩm cuối cùng lấy ra thuộc lô 1"
`C_2` là biến cố: "sản phẩm cuối cùng lấy ra thuộc lô 2"
\(\Rightarrow P\left(C_1\right)=\dfrac{2}{9};P\left(C_2\right)=\dfrac{7}{9}\)
`C_1`, `C_2` cũng là nhóm biến cố đầy đủ
\(P\left(B|C_1\right)=\dfrac{6}{9}=\dfrac{2}{3}\)
\(\Rightarrow P\left(C_1|B\right)=\dfrac{P\left(B|C_1\right).P\left(C_1\right)}{P\left(B\right)}=\dfrac{\dfrac{2}{3}.\dfrac{2}{9}}{\dfrac{19}{27}}=\dfrac{4}{19}\)
c.
\(P\left(A_2|B\right)=\dfrac{P\left(B|A_2\right).P\left(A_2\right)}{P\left(B\right)}=\dfrac{\dfrac{2}{3}.\dfrac{1}{2}}{\dfrac{19}{27}}=\dfrac{9}{19}\)

Gọi A, B, C lần lượt là các biến cố: "Khách hàng trả lời "sẽ sử dụng"."; "Khách hàng trả lời "có thể sẽ sử dụng"." và "Khách hàng trả lời "không sử dụng"." và X là biến cố: "Khách hàng sử dụng dịch vụ."
Khi đó theo đề bài, ta có \(P\left(A\right)=\dfrac{17}{100};P\left(B\right)=\dfrac{48}{100};P\left(C\right)=\dfrac{35}{100};P\left(X|A\right)=0,4;P\left(X|B\right)=0,2;P\left(X|C\right)=0,01\)
Theo công thức xác suất đầy đủ:
\(P\left(X\right)=P\left(A\right)P\left(X|A\right)+P\left(B\right)P\left(X|B\right)+P\left(C\right)P\left(X|C\right)\)
\(=\dfrac{17}{100}.0,4+\dfrac{48}{100}.0,2+\dfrac{35}{100}.0,01=\dfrac{67}{400}=0,1675=16,75\%\)
Vậy tỉ lệ khách hàng sử dụng dịch vụ là \(16,75\%\)
Gọi \(A_1\) là biến cố: "khách hàng được chọn thuộc nhóm trả lời sẽ sử dụng"
`A_2` là biến cố: "khách hàng được chọn thuộc nhóm trả lời có thể sẽ sử dụng"
`A_3` là biến cố: "khách hàng được chọn thuộc nhóm trả lời không sử dụng"
\(\Rightarrow P\left(A_1\right)=\dfrac{17}{100}\) ; \(P\left(A_2\right)=\dfrac{48}{100}\); \(P\left(A_3\right)=\dfrac{35}{100}\)
\(A_1;A_2;A_3\) tạo thành 1 nhóm biến cố đầy đủ
Gọi B là biến cố: "khách hàng đó sử dụng dịch vụ của công ty"
\(\Rightarrow P\left(B|A_1\right)=0,4\); \(P\left(B|A_2\right)=0,2\); \(P\left(B|A_3\right)=0,01\)
Theo công thức xác suất đầy đủ:
\(P\left(B\right)=0,4\times\dfrac{17}{100}+0,2\times\dfrac{48}{100}+0,01\times\dfrac{35}{100}=0,1675\)

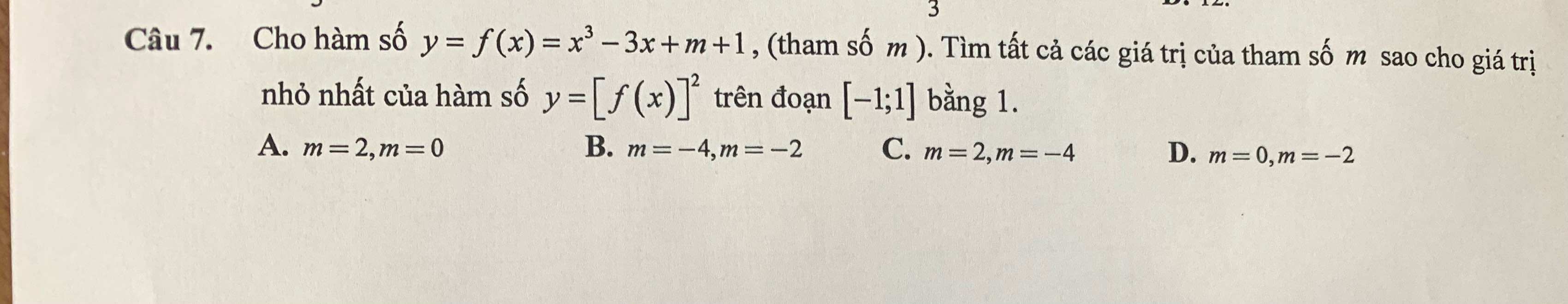
Ta có \(\sqrt{2+2\cos2x}=\sqrt{2+2\left(2\cos^2x-1\right)}=\sqrt{4\cos^2x}=2\left|\cos x\right|\)
\(\Leftrightarrow f\left(x\right)+f\left(-x\right)=2\left|\cos x\right|,\forall x\inℝ\) (1)
Đặt \(g\left(x\right)=f\left(x\right)-\left|\cos x\right|\)
Khi đó (1) \(\Leftrightarrow\left[f\left(x\right)-\left|\cos x\right|\right]+\left[f\left(-x\right)-\left|\cos x\right|\right]=0\)
\(\Leftrightarrow g\left(x\right)+\left[f\left(-x\right)-\left|\cos\left(-x\right)\right|\right]=0\) (do \(\cos x\) là hàm chẵn)
\(\Leftrightarrow g\left(x\right)+g\left(-x\right)=0\)
\(\Leftrightarrow g\left(x\right)=-g\left(-x\right)\)
\(\Leftrightarrow g\left(x\right)\) là hàm lẻ
Khi đó \(f\left(x\right)=g\left(x\right)+\left|\cos x\right|\) với \(g\left(x\right)\) là hàm lẻ. Thử lại, ta thấy:
(1) \(\Leftrightarrow f\left(x\right)+f\left(-x\right)=g\left(x\right)+\left|\cos x\right|+g\left(-x\right)+\left|\cos\left(-x\right)\right|\)
\(\Leftrightarrow f\left(x\right)+f\left(-x\right)=2\left|\cos x\right|\), thỏa mãn
Vậy \(f\left(x\right)=g\left(x\right)+\left|\cos x\right|\) với \(g\left(x\right)\) là hàm lẻ bất kì có tập xác định là \(ℝ\)
\(\Rightarrow I=\int\limits^{\dfrac{3\pi}{2}}_{-\dfrac{3\pi}{2}}f\left(x\right)dx\)
\(I=\int\limits^{\dfrac{3\pi}{2}}_{-\dfrac{3\pi}{2}}\left[g\left(x\right)+\left|\cos x\right|\right]dx\)
\(I=\int\limits^{\dfrac{3\pi}{2}}_{-\dfrac{3\pi}{2}}g\left(x\right)dx+\int\limits^{\dfrac{3\pi}{2}}_{-\dfrac{3\pi}{2}}\left|\cos x\right|dx\)
\(I=\int\limits^{\dfrac{3\pi}{2}}_{-\dfrac{3\pi}{2}}\left|\cos x\right|dx\) (do \(g\left(x\right)\) là hàm lẻ)
\(I=\int\limits^{-\dfrac{\pi}{2}}_{-\dfrac{3\pi}{2}}\left(-\cos x\right)dx+\int\limits^{\dfrac{\pi}{2}}_{-\dfrac{\pi}{2}}\cos xdx+\int\limits^{\dfrac{3\pi}{2}}_{\dfrac{\pi}{2}}\left(-\cos x\right)dx\)
\(I=-\sin x|^{-\dfrac{\pi}{2}}_{-\dfrac{3\pi}{2}}+\sin x|^{\dfrac{\pi}{2}}_{-\dfrac{\pi}{2}}-\sin x|^{\dfrac{3\pi}{2}}_{\dfrac{\pi}{2}}\)
\(I=6\)