Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Bài 11. Định lí và chứng minh định lí SVIP
1. Định lí. Giả thiết và kết luận của định lí.
Định lí là một khẳng định được suy ra từ những khẳng định đúng đã biết. Mỗi định lí thường được phát biểu dưới dạng:
Nếu ... thì...
- Phần giữa từ "nếu" và từ "thì" là giả thiết của định lí.
- Phần sau từ "thì" là kết luận của định lí.
Chẳng hạn, các tính chất của hai đường thẳng song song đã học đều là các định lí.
Ví dụ 1: Trong định lí "Một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó cũng vuông góc với đường thẳng còn lại", thì có:
+ Giả thiết là "một đường thẳng vuông góc với một trong hai đường thẳng song song".
+ Kết luận là "nó cũng vuông góc với đường thẳng còn lại".

Ta cũng có thể viết giả thiết và kết luận của định lí trên như sau:
| Giả thiết |
$d, \, d', \, d''$ là các đường thẳng, $d'$ // $d"$, $d \perp d'$ |
| Kết luận | $d \perp d"$ |
2. Thế nào là chứng minh định lí?
Chứng minh một định lí là dùng lập luận để từ giả thiết và những khẳng định đúng đã biết suy ra kết luận của định lí.
Ta chứng minh định lí: "Nếu một đường thẳng cắt hai đường thẳng song song thì hai góc đồng vị bằng nhau".
| Giả thiết | $a$ // $b$, $a$ cắt $c$ tại $A$, $b$ cắt $c$ tại $B$ |
| Kết luận | $\widehat{A_1} = \widehat{B_1}$ |
Chứng minh:
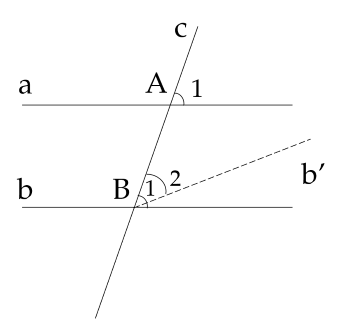
Qua điểm $B$ kẻ đường thẳng $b'$ sao cho góc $\widehat{B_2}=\widehat{A_1}$. Khi đó đường thẳng $c$ tạo với hai đường thẳng $a$ và $b'$ hai góc đồng vị bằng nhau $\widehat{A_1}=\widehat{B_2}$.
Theo dấu hiệu nhận biết hai đường thẳng song song ta có $a$ và $b'$ song song với nhau.
Suy ra qua $B$ có hai đường thẳng $b$ và $b'$ cùng song song với $a$. Theo tiên đề Euclid, hai đường thẳng $b$ và $b'$ trùng nhau. Từ đó suy ra $\widehat{B_1}=\widehat{A_1}$ (Vì cùng bằng $\widehat{B_2}$).

Bạn có thể đánh giá bài học này ở đây