Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Chứng minh định lí SVIP
Cho hai đường thẳng $x y$ // $x' y'$, đường thẳng ${d}$ cắt ${xy}$ và ${x}' {y}'$ tại ${A}$ và ${B}$. Kẻ tia phân giác ${AA}'$ của $\widehat{{xAB}}$ cắt $x' y'$ tại ${A}'$ và tia phân giác ${BB}'$ của $\widehat{{ABy}}'$ cắt $xy$ tại $B'$. Chứng minh rằng:
a) ${AA}' / / {BB}'$.
b) $\widehat{A A' B}=\widehat{A B' B}$.
Hướng dẫn giải:
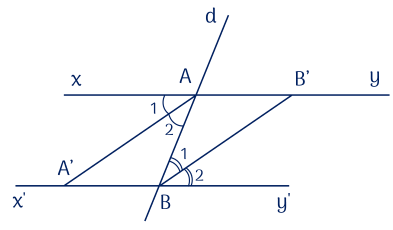
a) $xy$ // $x' y'$ nên $\widehat{xAB}=\widehat{ABy'}$ (hai góc so le trong). (1)
${AA}'$ là tia phân giác của $\widehat{xAB}$ nên: $\widehat{{A}_{1}}=\widehat{{A}_{2}}=\dfrac{1}{2} \widehat{{xAB}}$ (2)
${BB}'$ là tia phân giác của $\widehat{{ABy}'}$ nên: $\widehat{B_{1}}=\widehat{B_{2}}=\dfrac{1}{2} \widehat{A B y'} $ (3)
Từ (1), (2), (3) ta có: $\widehat{{A}_{2}}=\widehat{{B}_{1}}$.
Mà hai góc ở vị trí so le trong, nên ${AA}' // {BB}'$
b) $x y$ // $x' y'$ nên $\widehat{A_{1}}=\widehat{{AA}' {B}}$ (hai góc so le trong).
${AA}' / / {BB}'$ nên $\widehat{{A}_{1}}=\widehat{{AB}' {B}}$ (hai góc đồng vị).
Vậy $\widehat{{AA}' {B}}=\widehat{{AB}' {B}}$.
Chứng minh rằng: "Hai tia phân giác của hai góc đối đỉnh là hai tia đối nhau.
Hướng dẫn giải:
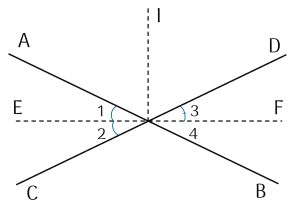
Theo đề bài:
$\widehat{{O}_{1}}=\widehat{{O}_{2}}$ ($OE$ là tia phân giác của $\widehat{AOC}) .$ (1)
$\widehat{{O}_{3}}=\widehat{{O}_{4}}$ ($OF$ là tia phân giác của $\widehat{DOB})$. (2)
Mà $\widehat{{AOD}}=\widehat{{COB}}$ (hai góc đối đỉnh).
Từ (1), (2), (3), ta có: $\widehat{{O}_{1}}+\widehat{{O}_{3}}+\widehat{{AOD}}=\widehat{{O}_{2}}+\widehat{{O}_{4}}+\widehat{{COB}}$ (4)
Mà $\left(\widehat{{O}_{1}}+\widehat{{O}_{3}}+\widehat{{AOD}}\right)+\left(\widehat{{O}_{2}}+\widehat{{O}_{4}}+\widehat{{COB}}\right)=360^{\circ}$. (5)
Do đó $\widehat{{O}_{1}}+\widehat{{O}_{3}}+\widehat{{AOD}}=180^{\circ}$.
Từ $(4)$ và $(5) \Rightarrow \widehat{{EOF}}=180^{\circ}$.
Vậy ${E}, {O}, {F}$ nằm trên một đường thẳng, hay tia ${OE}$ và tia ${OF}$ là hai tia đối nhau.
Cho hai đường thẳng $xy$ // $mn$, đường thẳng $a$ cắt hai đường thẳng $xy$ và $mn$ lần lượt tại ${A}$ và ${B}$. Kẻ tia phân giác của $\widehat{{xAB}}$ và tia phân giác của $\widehat{{ABm}}$, chúng cắt nhau tại ${C}$. Kẻ tia phân giác của $\widehat{{BAy}}$ và tia phân giác của $\widehat{{ABn}}$, chúng cắt nhau tại $D$. Chứng minh rằng:
a) ${AC} \perp {AD} ; {BD} \perp {BC}$.
b) ${AD} / / {BC} ; {AC} / / {BD}$.
c) Góc ${ACB}$ và góc $BDA$ là các góc vuông.
Hướng dẫn giải:
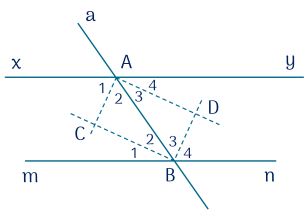
a) ${AC}$ và ${AD}$ là hai tia phân giác của hai góc kề bù, nên: ${AC} \perp {AD}$.
${BC}$ và ${BD}$ là hai tia phân giác của hai góc kề bù, nên: ${BC} \perp {BD}$.
b) Vì ${xy}$ // ${mn} \Rightarrow \widehat{{yAB}}=\widehat{{ABm}}$ (hai góc so le trong).
Vậy $\widehat{{A}_{3}}=\widehat{{B}_{2}}$ (cùng bằng $\dfrac{1}{2} \widehat{{yAB}}$ và $\dfrac{1}{2} \widehat{{ABm}}$).
Suy ra: ${AD} / / {BC}$.
$xy$ // ${mn} \Rightarrow \widehat{{xAB}}=\widehat{{ABn}}$ (hai góc so le trong).
Vậy $\widehat{{A}_{2}}=\widehat{{B}_{3}}$ (cùng bằng $\dfrac{1}{2} \widehat{{xAB}}$ và $\dfrac{1}{2} \widehat{{ABn}}$).
Suy ra: ${AC} / / {BD}$.
c) ${AD}$ // ${BD}$ (theo chứng minh b), ${BD} \perp {BC}$ (theo chứng minh a).
Vậy ${AD} \perp {BD}$ (${BD}$ vuông góc với một trong hai đường song song thì vuông góc với đường còn lại).
Suy ra: $\widehat{{ADB}}=90^{\circ}$.
Tương tự: ${AD}$ // ${BC}$ (theo chứng minh b); ${AD} \perp {AC}$ (theo chứng minh a).
Vậy ${AC} \perp {BC}$ (như trên).
Suy ra: $\widehat{{ACB}}=90^{\circ}$.
Cho $\triangle {ABC}$ và ${AE}$ là tia phân giác của $\widehat{A}$ $({E}$ thuộc ${BC})$. Từ ${E}$ kẻ ${EF}$ // ${AB}$ ($F$ thuộc $AC$). Từ $F$ kẻ $FI$ // $AE$ ($I$ thuộc $BC$). Chứng minh:
1) $\widehat{{BAE}}=\widehat{{EAC}}=\widehat{{AEF}}=\widehat{{EFI}}=\widehat{{IFC}}$.
2) $FI$ là tia phân giác của $\widehat{{EFC}}$.
Hướng dẫn giải:
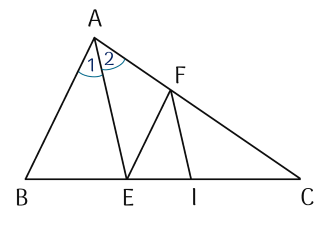
1) $\widehat{{BAE}}=\widehat{{EAC}}$ (giả thiết). (1)
Vì ${AB}$ // ${EF}$ nên $\widehat{{BAE}}=\widehat{{AEF}}$ (hai góc so le trong). (2)
Vì $AE$ // $FI$ nên $\widehat{EAC}=\widehat{IFC}$ (hai góc đồng vị). (3)
Vì ${AE}$ // ${FI}$ nên $\widehat{{AEF}}=\widehat{{EFI}}$ (hai góc so le trong). (4)
Từ (1), (2), (3), (4) suy ra: $\widehat{{BAE}}=\widehat{{EAC}}=\widehat{{AEF}}=\widehat{{IFC}}=\widehat{{EFI}}$.
2) Từ chứng minh trên, ta có: $\widehat{{EFI}}=\widehat{{IFC}}$ mà ${FI}$ là tia nằm giữa hai tia ${FE}$ và ${FC}$.
Vậy ${FI}$ là tia phân giác của $\widehat{{EFC}}$.
