Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Chứng minh hai đường thẳng song song SVIP
Cho hình vẽ sau:
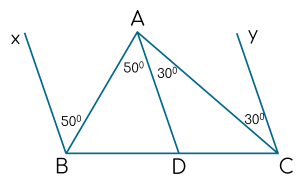
Chứng minh $Bx$ // $Cy$.
Hướng dẫn giải:

Ta có $\widehat{xBA} = \widehat{BAD} = 50^{\circ}$.
Hai góc này ở vị trí so le trong nên $Bx$ // $AD$ (1).
Ta có $\widehat{DAC} = \widehat{ACy} = 30^{\circ}$.
Hai góc này ở vị trí so le trong nên $Cy$ // $AD$ (2).
Từ (1) và (2) suy ra $Bx$ // $Cy$ (cùng song song với $AD$).
Cho hình vẽ:
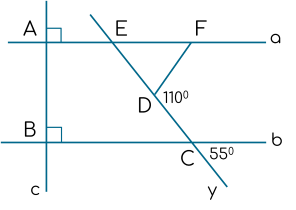
Biết $a \perp c$; $b \perp c$; $\widehat{FDC} = 110^{\circ}$ và $\widehat{bCy} = 55^{\circ}$.
a) Chứng minh $a$ // $b$.
b) Kẻ tia $Dn$ là tia phân giác của $\widehat{FDC}$. Chứng minh $Dn$ // $a$.
Hướng dẫn giải:
a) Ta có $a \perp c$ và $b \perp c$ nên $a$ // $b$ (tính chất từ vuông góc đến song song).
b)
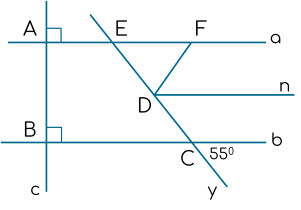
Ta có $\widehat{bCy} = \widehat{ECB} = 55^{\circ}$.
Vì $a$ // $b$ nên $\widehat{ECB} = \widehat{FED} = 55^{\circ}$.
Vì $Dn$ là tia phân giác của $\widehat{FDC}$ nên $\widehat{CDn} = \dfrac12.\widehat{FDC} = 55^{\circ}$.
Nên $\widehat{FED} =\widehat{CDn}$ mà hai góc này ở vị trí đồng vị nên $Dn$ // $a$.
Cho tam giác $ABC$ có $\widehat{A} = 90^{\circ}$. Kẻ $AH \perp BC$ với $H \in BC)$. Kẻ $HE \perp AC$ với $E \in AC$.
a) Chứng minh $AB$ // $HE$.
b) Biết $\widehat{B} = 60^{\circ}$. Tính $\widehat{AHE}$, $\widehat{BAH}$.
