Chứng minh hai góc đối đỉnh SVIP

Hướng dẫn giải:

Vì $\widehat{AOD}$ và $\widehat{BOC}$ đối đỉnh nên $\widehat{AOD}=\widehat{BOC}$.

Mà $\widehat{AOD}+\widehat{BOC}=100^{\circ}$ nên $\widehat{AOD}=\widehat{BOC}=100^{\circ}: 2=50^{\circ}$.

Lại có $\widehat{BOD}$ và $\widehat{BOC}$ kề bù nên $\widehat{BOD}+\widehat{BOC}=180^{\circ}$.

Suy ra $\widehat{BOD}=180^{\circ}-\widehat{BOC}=180^{\circ}-50^{\circ}=130^{\circ}$.

Suy ra $\widehat{AOC} = \widehat{BOD}=130^{\circ}$ (hai góc đối đinh).

Hướng dẫn giải:

Vi $O$ nằm trên đường thẳng $x x'$ nên hai tia $O x$ và $O x'$ là hai tia đối nhau. (1)

Do $O N$ và $O M$ thuộc hai nửa mặt phẳng đối nhau bờ $O x$ nên tia $O x$ nằm giữa $O N$ và $O M$.

Suy ra $\widehat{xOM}+\widehat{xON}=140^{\circ}+40^{\circ}=180^{\circ}$.

Vậy $\widehat{x OM}$ và $\widehat{xO N}$ là hai góc kề bù.

Suy ra hai tia $O M$ và $O N$ đối nhau. (2)

Từ (1) và (2), suy ra $\widehat{xO N}$ và $\widehat{x' O M}$ là hai góc đối đỉnh.

Hướng dẫn giải:

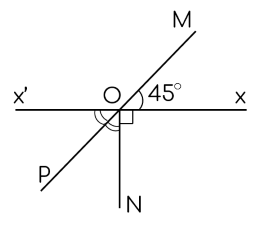
Vi $\widehat{xON}$ và $\widehat{x' O N}$ kề bù nên $\widehat{x O N}+\widehat{x' ON}=180^{\circ}$.

Mà $\widehat{x O N}=90^{\circ}$ nên $\widehat{x' ON}=90^{\circ}$.

Vì tia $O P$ là tia phân giác của góc $\widehat{x'ON}$ nên $\widehat{x' OP}=\widehat{PO N}=\dfrac{1}{2} \widehat{x'O N}=45^{\circ}$.

Mặt khác hai tia $O P$ và $O M$ thuộc hai nửa mặt phẳng đối nhau bờ $x x'$ nên $\widehat{M O P}=\widehat{P ON}+\widehat{xO N}+\widehat{x OM}=45^{\circ}+90^{\circ}+45^{\circ}=180^{\circ}$.

Suy ra hai tia $O P$ và $O M$ là hai tia đối nhau. Mà $O x$ và $O x'$ là hai tia đối nhau.

Suy ra $\widehat{x O M}$ và $\widehat{x' OP}$ là hai góc đối đỉnh.

Hướng dẫn giải:

Vơi $n$ đường thẳng cắt nhau tại một điểm, ta có $2 n$ tia chung gồc.

Chọn $1$ tia trong $2 n$ tia chung gốc đó, tạo với $2 n-1$ tia còn lại, ta được $2 n-1$ (góc).

Làm như vậy với $2 n$ tia chung gốc, ta được $2 n.(2 n-1)$ (góc).

Nhưng vì mỗi góc đã được tính hai lần nên số góc thực tế là $\dfrac{2 n.(2 n-1)}{2}=n.(2 n-1)$ (góc).

Vì có $n$ đường thẳng nên sẽ có $n$ góc bẹt.

Do đó số góc khác góc bẹt là $n.(2 n-1)-n=n.(2 n-2)$ (góc).

Mỗi góc trong số $n.(2 n-2)$ góc đó đều có một góc đối đỉnh với nó.

Suy ra số cặp góc đối đỉnh là $\dfrac{n(2 n-2)}{2}=n.(n-1)$.

Vậy với $n$ đường thẳng cắt nhau tại một điểm, ta được $n.(n-1)$ cặp góc đối đỉnh.

Hướng dẫn giải:

Có $\widehat{B O C}$ và $\widehat{BO D}$ là hai góc kề bù nên $\widehat{BO C}+ \widehat{BO D}=180^{\circ}$.

Vì $O M$ là tia phân giác của $\widehat{BO C} $ nên $\widehat{CO M}=\widehat{M O B}=\dfrac{1}{2} \widehat{BO C}$;

$O N$ là tia phân giác của góc $\widehat{B OD}$ nên $\widehat{D ON}=\widehat{N O B}=\dfrac{1}{2} \widehat{B O D} .$

Mà tia $O B$ nằm giữa tia $O M$ và $O N$.

Suy ra $\widehat{M O N}=\widehat{M O B}+\widehat{N O B}=\dfrac{1}{2}(\widehat{B O C}+\widehat{B OD})=\dfrac{1}{2}. 180^{\circ}=90^{\circ}$.

Mặt khác $\widehat{M O P}=90^{\circ}$ (tia $O P$ vuông góc $O M$ ).

Suy ra $\widehat{M O N}+\widehat{M O P}=90^{\circ}+90^{\circ}=180^{\circ}$.

Mà hai tia $O P$ và $O N$ nằm trền hai nửa mặt phẳng bờ $O M$ nên hai tia $O P$ và $O N$ là hai tia đối nhau.

Kết hợp $O C$ và $O D$ là hai tia đối nên suy ra $\widehat{C O P}$ và $ \widehat{DO N}$ là hai góc đối đỉnh.