Đề thi học kì II - Phòng GD Bắc Từ Liêm - Hà Nội (2021) SVIP

Hướng dẫn giải:

1. Với $x=49 \Rightarrow A=\frac{4 \sqrt{49}}{\sqrt{49}-1}=\frac{4.7}{6}=14$.
Xét $B=\frac{1}{\sqrt{x}+1}+\frac{\sqrt{x}}{\sqrt{x}-1}+\frac{2}{x-1}=\frac{\sqrt{x}-1+\sqrt{x}(\sqrt{x}+1)+2}{x-1}=\frac{\sqrt{x}-1+x+\sqrt{x}+2}{x-1}$
$\Rightarrow B=\frac{\sqrt{x}-1+x+\sqrt{x}+2}{x-1}=\frac{(\sqrt{x}+1)^{2}}{(\sqrt{x}-1)(\sqrt{x}+1)}=\frac{\sqrt{x}+1}{\sqrt{x}-1}$
3. Ta có $P=A: B=\frac{4 \sqrt{x}}{\sqrt{x}-1}: \frac{\sqrt{x}+1}{\sqrt{x}-1}=\frac{4 \sqrt{x}}{\sqrt{x}+1}$
Khi đó $P(\sqrt{x}+1)=x+4+\sqrt{x-4}$
Điều kiện: $x \geq 4$ Nên $\frac{4 \sqrt{x}}{\sqrt{x}+1}(\sqrt{x}+1)=x+4+\sqrt{x-4} \Rightarrow 4 \sqrt{x}=x+4+\sqrt{x-4}$
$\Rightarrow 4 \sqrt{x}=x+4+\sqrt{x-4} \Leftrightarrow x+4+\sqrt{x-4}-4 \sqrt{x}=0 \Leftrightarrow(\sqrt{x}-2)^{2}+\sqrt{x-4}=0$
Do $\left\{\begin{array}{l}(\sqrt{x}-2)^{2} \geq 0 \\ \sqrt{x-4} \geq 0\end{array} \Rightarrow 4 \sqrt{x}=x+4+\sqrt{x-4} \Leftrightarrow(\sqrt{x}-2)^{2}+\sqrt{x-4} \geq 0\right.$
Dầu " $="$ xay ra $\Leftrightarrow\left\{\begin{array}{l}\sqrt{x}-2=0 \\ \sqrt{x-4}=0\end{array} \Leftrightarrow\left\{\begin{array}{l}\sqrt{x}=2 \\ x-4=0\end{array} \Leftrightarrow x=4(t m)\right.\right.$
Vậy $x=4$ thì $P(\sqrt{x}+1)=x+4+\sqrt{x-4}$.

Hướng dẫn giải:

Gọi chiều dài ban đầu của mảnh vườn là $x(m)$, chiều rộng ban đầu là $y(m) .(x>y>0)$ Vì chu vi ban đầu của mảnh vườn là $124 m$ nên ta có phương trình: $2(x+y)=124$ $\Leftrightarrow x+y=62(1)$
Sau khi thay đổi kích thước thì chiều dài mảnh vườn là: $(x+5)(m)$ và chiều rộng là: $(y+3)(m)$. Diện tích mảnh vườn tăng thêm $255 m^{2}$ nên ta có phương trình: $(x+5)(y+3)=\mathrm{xy}+255$. $\Leftrightarrow 3 x+5 y=240$
Từ (1), (2) ta có hệ : $\left\{\begin{array}{l}x+y=62 \\ 3 x+5 y=240\end{array} \Leftrightarrow\left\{\begin{array}{l}3 x+3 y=186 \\ 3 x+5 y=240\end{array} \Leftrightarrow\left\{\begin{array}{l}y=27 \\ x=35\end{array}\right.\right.\right.$ ( thỏa mãn điều kiện)
Vậy chiều dài ban đầu của mảnh vườn là $35 m$, chiều rộng là $27 m$.

Hướng dẫn giải:

Bán kính mặt bàn là : $R=\frac{1,2}{2}=0,6(m$ ).

Diện tích mặt bàn là : $S=\pi R^{2} \approx 3,14 \cdot(0,6)^{2} \approx 1,13\left(m^{2}\right)$

Hướng dẫn giải:

$\left\{\begin{array}{l}2(x+2)-\sqrt{y-1}=6 \\ 5(x+2)-2 \sqrt{y-1}=16\end{array} \quad\right.$ (ĐKXĐ: $y \geq 1$ )
Đặt $\left\{\begin{array}{l}x+2=a \\ \sqrt{y-1}=b(b \geq 0)\end{array}\right.$ khi đó hệ phương trình trở thành $\left\{\begin{array}{l}2 a-b=6 \\ 5 a-2 b=16\end{array}\right.$
$\Leftrightarrow\left\{\begin{array}{l}4 a-2 b=12 \\ 5 a-2 b=16\end{array}\right.$
$\Leftrightarrow\left\{\begin{array}{l}a=4 \\ 2 a-b=6\end{array}\right.$
$\Leftrightarrow\left\{\begin{array}{l}a=4 \\ 2.4-b=6\end{array}\right.$
$\Leftrightarrow\left\{\begin{array}{l}a=4 \\ b=2\end{array}\right.$ (tmđk $\left.b \geq 0\right)$
$\Leftrightarrow\left\{\begin{array}{l}x+2=4 \\ \sqrt{y-1}=2\end{array}\right.$
$\Leftrightarrow\left\{\begin{array}{l}x=2 \\ y-1=4\end{array}\right.$
$\Leftrightarrow\left\{\begin{array}{l}x=2 \\ y=5\end{array}(\text{tm đkxđ})\right.$
Vậy hệ phương trình có nghiệm $(x ; y)$ là $(2 ; 5)$

Hướng dẫn giải:

a) Thay $\mathrm{m}=2$ vào phương trình đường thẳng (d) ta có $y=2 x+3$
Phương trình hoành độ giao điểm hai đồ thị hàm số (P) và (d) là $x^{2}=2 x+3$
$\Leftrightarrow x^{2}-2 x-3=0$

$\Rightarrow \Delta>0$
$\Rightarrow$ phương trình có hai nghiệm phân biệt
Thay $x_{1}=3$ vào phương trình (P) ta có $y_{1}=9$ Thay $x_{2}=-1$ vào phương trình $(P)$ ta có $y_{2}=1$ độ giao điểm hai đồ thị hàm số (P) và (d) là $(3 ; 9)$ và $(-1 ; 1)$

b) $x^{2}=m x+3$
$\Leftrightarrow x^{2}-m x-3=0$
$\Delta=b^{2}-4 a c$
$=m^{2}-4.1 \cdot(-3)=m^{2}+12$
$m^{2}+12 \geq 12>0$
$\Rightarrow \Delta>0$
Suy ra phương trình có hai nghiệm phân biệt với mọi $m$.

Do đó (d) cắt (P) tại hai điểm phân biệt với mọi $m$.

+) Áp dụng hệ thức Vi et ta có $S=x_{1}+x_{2}=\frac{-b}{a}=m$
$P=x_{1} \cdot x_{2}=\frac{c}{a}=-3$
1 $x_{1} x_{2}=-3 \Rightarrow x_{1} x_{2} \neq 0$ nên $x_{1} \neq 0$ và $x_{2} \neq 0$
có $\frac{1}{x_{1}}+\frac{1}{x_{2}}=\frac{3}{2}$
$\Leftrightarrow \frac{x_{1}+x_{2}}{x_{1} x_{2}}=\frac{3}{2}$
$\Leftrightarrow 2\left(x_{1}+x_{2}\right)=3 x_{1} x_{2}$
$\Rightarrow 2 m=3(-3)$
$\Leftrightarrow m=\frac{-9}{2}$
Vậy (d) cắt (P) tại hai điểm phân biệt có hoành độ $x_{1} ; x_{2}$ thỏa mãn $\frac{1}{x_{1}}+\frac{1}{x_{2}}=\frac{3}{2} \Leftrightarrow m=\frac{-9}{2}$ .

Hướng dẫn giải:

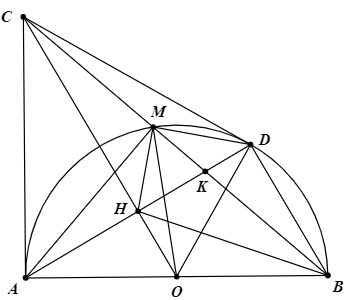
1) Tứ giác $A C D O$ có $\widehat{C A O}=\widehat{CDO}=90^{\circ}$ (tính chất của tiếp tuyến ) nên tử giác $A C D O$ nội tiếp đường tròn đường kính $A O$.

2)
Xét $\Delta C D M$ và $\Delta C B D$ có:
$\widehat{M C D}$ chung:
$\widehat{C D M}=\widehat{CBD}$ (góc nội tiếp và góc tạo bời tia tiếp tuyến và dây cung cùng chắn $\overgroup{M D}$ ) $\Rightarrow \Delta C D M \backsim \Delta C B D \Rightarrow \dfrac{C D}{C M}=\dfrac{C B}{C D} \Leftrightarrow C D^{2}=C M \cdot C B$

3) Theo tính chất hai tiếp tuyến cắt nhau, ta có $C A=C D$ mà $O A=O D(=R)$ nên $O C$ là trung trực của $A D \Rightarrow O C \perp A D$ tại trung điểm $H$ của $A D$.

Lại có $A M B=90^{\circ}$ (góc nội tiếp chắn nửa đường tròn) $\Rightarrow \widehat{AM C}=90^{\circ}$ (kề bù với $\widehat{A M B}$ ).

Tứ giác $A C M H$ có $\widehat{A M C}=\widehat{A H C}=90^{\circ}$ nên nội tiếp đường tròn đường kính $A C$ $\Rightarrow \widehat{M H C}=\widehat{M A C}$ (hai góc nội tiếp cùng chắn $\overrightarrow{M C}$ ), mà $\widehat{M A C}=\widehat{M B A}$ (góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cung cùng chắn $\overgroup{A M}$)

$\Rightarrow \widehat{M H C}=\widehat{M B A}(=\widehat{M A C})$ hay $\widehat{M H C}=\widehat{CBO}$.
Vì $\widehat{M HC}=\widehat{C B O}$ nên tứ giác $O H M B$ nội tiếp (có góc ngoài đỉnh $H$ bằng góc trong đỉnh $B$) 

$\Rightarrow \widehat{OHB}=\widehat{O M B}$ (hai góc nội tiếp cùng chắn $\overgroup{O B}$ ) và $\widehat{O M B}=\widehat{M B O}(\Delta O M B$ cân tại $O)$.

Vậy $\widehat{M H C}=\widehat{M B O}=\widehat{O M B}=\widehat{OHB} \Rightarrow 90^{\circ}-\widehat{M HC}=90^{\circ}-\widehat{OHB} \Rightarrow \widehat{M H K}=\widehat{B H K}$

$\Rightarrow H K$ là tia phân giác trong tại đỉnh $H$ của $\Delta M H B$.

Lại có $H C \perp H K \Rightarrow H C$ là phân giác ngoài tại đỉnh $H$ của $\Delta M H B$.

Theo tính chất đường phân giác, ta có: $\dfrac{C M}{C B}=\dfrac{H M}{H B}=\dfrac{K M}{K B}$. Vậy $\dfrac{C M}{C B}=\dfrac{K M}{K B}$.

Hướng dẫn giải:

Áp dụng bất đẳng thức $\dfrac{1}{x}+\dfrac{1}{y} \geq \dfrac{4}{x+y}, x, y>0$.

Dấu "=" xảy ra $\Leftrightarrow x=y$. ( Chứng minh bằng phương pháp biến tổi tươg đuơng)

Ta có : $M=\dfrac{1}{a^{2}+b^{2}}+\dfrac{2}{a b}+4 a b$
$=\dfrac{1}{a^{2}+b^{2}}+\dfrac{1}{2 a b}+\dfrac{3}{2 a b}+4 a b$
$=\left(\dfrac{1}{a^{2}+b^{2}}+\dfrac{1}{2 a b}\right)+\left(4 a b+\dfrac{1}{4 a b}\right)+\dfrac{5}{4 a b}$
+) $\quad \dfrac{1}{a^{2}+b^{2}}+\dfrac{1}{2 a b} \geq \dfrac{4}{(a+b)^{2}} \geq 4$
+) $\quad 4 a b+\dfrac{1}{4 a b} \geq 2 \sqrt{4 a b \cdot \dfrac{1}{4 a b}}=2$
+) $\quad 2 \sqrt{a b} \leq a+b \leq 1 \Leftrightarrow a b \leq \dfrac{1}{4} \Leftrightarrow \dfrac{1}{a b} \geq 4 \Leftrightarrow \dfrac{5}{4 a b} \geq 5$
Suy ra: $M \geq 4+2+5=11 .$

Dấu "=" xảy ra khi $a=b=\dfrac{1}{2}$.

Vậy GTNN của $M=11$ khi $a=b=\dfrac{1}{2}$.