Đề thi học kì II - Thành phố Huế (2021) SVIP

Hướng dẫn giải:

a)

Vì $R=\frac{1}{2} \cdot 1,4=0,7(\mathrm{~m})$ và $h=1,5(\mathrm{~m})$ nên thể tích của bồn chứa nước đó bằng: $ V=\pi R^{2} h=\pi \cdot(0,7)^{2} \cdot 1,5=\frac{147 . \pi}{200}=0,735 . \pi\left(m^{3}\right)$.

Vậy $V=0,735 . \pi\left(m^{3}\right) \text { . } $

b) 

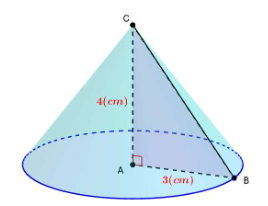
$\Delta A B C$ vuông tại $A ; B C=\sqrt{A B^{2}+A C^{2}}=5(\mathrm{~cm}) .$
Khi quay $\Delta A B C$ quanh cạnh $A C$ cố định, ta được hình nón có chiều cao $A C$, đường $\sinh l=B C$ và bán kính đáy $R=A B$. Diện tích xung quanh: $S_{x q}=\pi R . l=\pi .3 .5=15 \pi\left(\mathrm{cm}^{2}\right)$.
Vậy $S_{x q}=15 \pi\left(\mathrm{cm}^{2}\right)$.
$\Delta A B C \text { vuông tại } A  B C=\sqrt{A B^{2}+A C^{2}}=5(\mathrm{~cm})$.

Hướng dẫn giải:

a) $x_{1}=-4$ là nghiệm của phương trình nên: $(-4)^{2}-(-4) m-10 m+2=0 \Leftrightarrow-6 m+18=0 \Leftrightarrow m=3$.
Khi $m=3$, phương trình trở thành: $x^{2}-3 x-28=0$
Ta có, $\Delta=(-3)^{2}-4 \cdot(-28)=121>0$
Phương trình có hai nghiệm: $\left[\begin{array}{l}x_{1}=\frac{3-11}{2}=-4 \\ x_{2}=\frac{3+11}{2}=7\end{array}\right.$.
Vậy $m=3$ và nghiệm còn lại $x_{2}=7$
b) Ta có: $\Delta=b^{2}-4 a c=(-6)^{2}-4.7=8>0$ nên phương trình luôn có hai nghiệm phân biệt.
Gọi $x_{1}, x_{2}$ là hai nghiệm của phương trình.
Áp dụng hệ thức Viet, ta có: $\left\{\begin{array}{l}x_{1}+x_{2}=6 \\ x_{1} x_{2}=7\end{array}\right.$.

Hướng dẫn giải:

a) $x^{2}-(m+2) x+m=0$
(1).
$\Delta=(m+2)^{2}-4 m=m^{2}+4 m+4-4 m=m^{2}+4>0$ với mọi m.
Vậy phương trình (1) luôn có hai nghiệm phân biệt với mọi giá trị của $\mathrm{m}$.
Theo Viet: $\left\{\begin{array}{c}x_{1}+x_{2}=m+2 \\ x_{1} \cdot x_{2}=m\end{array}\right.$.
$x_{1}+x_{2}-3 x_{1} x_{2}=2 \Leftrightarrow m+2-3 m=2 \Leftrightarrow m=0 .$
Vậy $m=0$ thì phương trình (1) có hai nghiệm $x_{1}, x_{2}$ thỏa mãn hệ thức $x_{1}+x_{2}-3 x_{1} x_{2}=2$.

Hướng dẫn giải:

Gọi $x$ là độ dài cạnh cần tìm $(0<x<360$, đơn vị: $m$ )
Chiều cao tương ứng là $\frac{360}{x}(m)$.
Đô dài cạnh đó sau khi tăng là $x+4(m)$
Chiều cao tương ứng sau khi tăng là $\frac{360}{x}-1(\mathrm{~m})$.
Diện tích thửa ruộng không đổi nên ta có phương trình
$\frac{1}{2}(x+4)\left(\frac{360}{x}-1\right)=180 \Leftrightarrow x^{2}+4 x-1440=0$

Giải phương trình ta được $x=36(\mathrm{tm}), x=-40(\mathrm{ktm})$
Vậy độ dài cạnh cần tìm là $36 m$.

Hướng dẫn giải:

a) Vì $A C B$ là góc nội tiếp chắn nửa đường tròn nên $\widehat{A C B}=90^{\circ} .$ Suy ra $\widehat{A C M}=90^{\circ}$
Tứ giác $A H M C$ có $\widehat{A C M}+\bar{A} \bar{H} \bar{M}=90^{\circ}+90^{\circ}=180^{\circ}$ nên tứ giác $A H M C$ nội tiếp (đpcm).
b) Trong $(O)$, ta có: $\widehat{AD C}=\widehat{A B C}$ (góc nội tiếp cùng chắn cung $\overgroup{A C}$ )

Tứ giác $A H M C$ nội tiếp nên $\widehat{A M H}=\widehat{A C H}$ (góc nội tiếp củng chắn cung $\widehat{A H}$ ).
Vì $M H$ song song với $C D$ nên $\widehat{A D C}=\widehat{A M H}$ ( 2 góc so le trong).
Từ đó suy ra, $\widehat{A M H}=\widehat{A B C}($ đpcm $)$.
c) Ta có: $\widehat{C O B}=180^{\circ}-45^{\circ}=135^{\circ}$ nên sđ $\widehat{B C}=135^{\circ}$.
Lại có: $R=2 \mathrm{~cm}$ suy ra diện tích cần tìm là $S=\frac{\pi R^{2} n}{360}=\frac{\pi \cdot 2^{2} \cdot 135}{360}=\frac{3}{2} \pi\left(\mathrm{cm}^{2}\right)$.