Mở đầu về đường tròn SVIP

1. Đường tròn

Định nghĩa

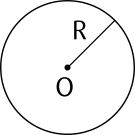
Đường tròn tâm $O$ bán kính $R$ ($R > 0$), kí hiệu là $(O ; R)$ là hình gồm tất cả các điểm cách điểm $O$ một khoảng bằng $R$.

Chú ý

+ Khi không cần để ý tới bán kính, ta kí hiệu đường tròn tâm $O$ là $(O)$.

+ Nếu $A$ là một điểm của đường tròn $(O)$ thì ta viết $A \in (O)$. Ta còn nói $(O)$ đi qua điểm $A$ hay điểm $A$ nằm trên đường tròn $(O)$.

Ví dụ 1. Gọi tên, xác định tâm và bán kính của các đường tròn trong hình vẽ sau:

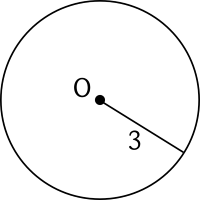
Lời giải

Đường tròn $(O ; 3)$ có tâm $O$ và bán kính bằng $3$.

Ví dụ 2. Gọi $O$ là trung điểm của đoạn thẳng $AB$. Chứng minh đường tròn $(O ; OA)$ đi qua $B$.

Lời giải

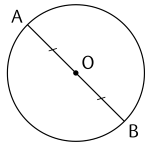
Vì $O$ là trung điểm của $AB$ nên $OB = OA$.

Do đó, $B \in (O ; OA)$ hay đường tròn $(O ; OA)$ đi qua $B$.

Nhận xét

i) Đoạn thẳng $AB$ là đường kính của $(O)$ nên $(O)$ còn gọi là đường tròn đường kính $AB$.

ii) Điểm $A$ nằm trên, điểm $C$ nằm trong và điểm $B$ nằm ngoài đường tròn.

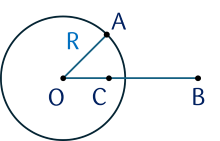
+ Điểm $M$ nằm trên đường tròn $(O ; R)$ nếu $OM = R$;

+ Điểm $M$ nằm trong đường tròn $(O ; R)$ nếu $OM < R$;

+ Điểm $M$ nằm ngoài đường tròn $(O ; R)$ nếu $OM > R$.

iii) Hình tròn tâm $O$ bán kính $R$ là hình gồm các điểm nằm trên và nằm trong đường tròn $(O ; R)$.

2. Tính đối xứng của đường tròn

Nhận xét

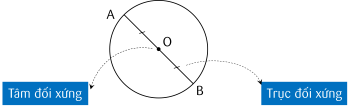
 + Đường tròn là hình có tâm đối xứng, tâm của đường tròn là tâm đối xứng của đường tròn đó.

+ Đường tròn là hình có trục đối xứng. Mỗi đường thẳng đi qua tâm là một trục đối xứng của đường tròn đó.

Ví dụ 3. Cho đường tròn $(I)$, tìm tâm đối xứng của $(I) $ và vẽ hai trục đối xứng của $(I)$.

Lời giải

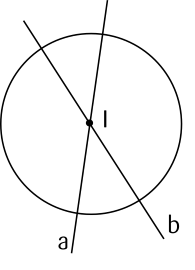
+ Tâm $I$ là tâm đối xứng của $(I)$;

+ Vẽ hai đường thẳng $a$ và $b$ đi qua tâm $I$.

Ta có $a$ và $b$ đều là trục đối xứng của $(I)$.