Phần tự luận (7 điểm) SVIP

Hướng dẫn giải:

a) $\underset{x\to 2}{\mathop{\lim }}\,\left( \sqrt{x+2}+2018 \right)=\sqrt{2+2}+2018=2020$.

b) $\underset{n\to +\infty }{\mathop{\lim }}\,\dfrac{{{3.4}^{n}}+{{2}^{n}}}{{{5.4}^{n}}+{{3}^{n}}}=\underset{n\to +\infty }{\mathop{\lim }}\,\dfrac{3+\dfrac{{{2}^{n}}}{{{4}^{n}}}}{5+\dfrac{{{3}^{n}}}{{{4}^{n}}}}=\underset{n\to +\infty }{\mathop{\lim }}\,\dfrac{3+{{\left( \dfrac{1}{2} \right)}^{n}}}{5+{{\left( \dfrac{3}{4} \right)}^{n}}}=\dfrac{3}{5}$.

c) $\underset{x\to -3}{\mathop{\lim }}\,\dfrac{{{x}^{2}}+4x+3}{{{x}^{2}}-9}=\underset{x\to -3}{\mathop{\lim }}\,\dfrac{\left( x+1 \right)\left( x+3 \right)}{\left( x-3 \right)\left( x+3 \right)}=\underset{x\to -3}{\mathop{\lim }}\,\dfrac{x+1}{x-3}=\dfrac{-3+1}{-3-3}=\dfrac{1}{3}$.

Hướng dẫn giải:

a) $y={{x}^{3}}-3{{x}^{2}}+2020x$.

+ Tập xác định: $D=\mathbb{R}$.

+ ${y}'={{\left( {{x}^{3}}-3{{x}^{2}}+2020x \right)}'}$$={{\left( {{x}^{3}} \right)}'}-{{\left( 3{{x}^{2}} \right)}'}+{{\left( 2020x \right)}'}$$=3{{x}^{2}}-6x+2020$.

+ Vậy ${y}'=3{{x}^{2}}-6x+2020$.

b) $y=\cos 3x-\sin x$.

+ Tập xác định: $D=\mathbb{R}$.

+ ${y}'={{\left( \cos 3x-\sin x \right)}'}$$={{\left( \cos 3x \right)}'}-{{\left( \sin x \right)}'}$$=-{{\left( 3x \right)}'}\sin 3x-\cos x$$=-3\sin 3x-\cos x$.

+ Vậy ${y}'=-3\sin 3x-\cos x$.

Hướng dẫn giải:

Tập xác định: $D=\mathbb{R}\backslash \left\{ 1 \right\}$.

Gọi (d) là tiếp tuyến của (C) và (d) song song với (d’): $y=-3x+2020$.

Ta có: ${f}'(x)=\dfrac{-3}{{{\left( x-1 \right)}^{2}}},$ $\forall x\in D$.

Gọi $M\left( {{x}_{0}};\,{{y}_{0}} \right)$ là tiếp điểm của (C) và (d).

Suy ra hệ số góc của tiếp tuyến (d): ${f}'({{x}_{0}})=\dfrac{-3}{{{\left( {{x}_{0}}-1 \right)}^{2}}}$.

Vì (d) song song với (d’) nên ${f}'({{x}_{0}})=-3  \Leftrightarrow   \dfrac{-3}{{{\left( {{x}_{0}}-1 \right)}^{2}}}=-3$. $\Leftrightarrow   {{\left( {{x}_{0}}-1 \right)}^{2}}=1$   

$\Leftrightarrow   \left[ \begin{aligned} & {{x}_{0}}-1=1 \\ & {{x}_{0}}-1=-1 \\ \end{aligned} \right.$  $\Leftrightarrow   \left[ \begin{aligned} & {{x}_{0}}=2 \\ & {{x}_{0}}=0 \\ \end{aligned} \right.$.

+ Với ${{x}_{0}}=2\Rightarrow {{y}_{0}}=\dfrac{2.2+1}{2-1}=5$.

Phương trình tiếp tuyến (d) có dạng: $y={f}'({{x}_{0}})\left( x-{{x}_{0}} \right)+{{y}_{0}}$ $\Leftrightarrow   y=-3\left( x-2 \right)+5$  $\Leftrightarrow   y=-3x+11$.

+ Với ${{x}_{0}}=0\Rightarrow {{y}_{0}}=\dfrac{2.0+1}{0-1}=-1$

Phương trình tiếp tuyến (d) có dạng: $y={f}'({{x}_{0}})\left( x-{{x}_{0}} \right)+{{y}_{0}}$ $\Leftrightarrow   y=-3\left( x-0 \right)-1$ $\Leftrightarrow y=-3x-1$.

Vậy có hai tiếp tuyến thỏa mãn yêu cầu bài toán là: $({{d}_{1}}):y=-3x+11$ và $({{d}_{2}}):y=-3x-1$.

Hướng dẫn giải:

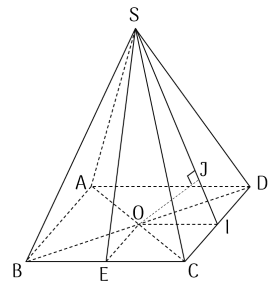
a) Vì đáy $ABCD$ là hình vuông nên $BD\bot AC$.

Do $\left\{ \begin{aligned} & BD\bot AC \\ & BD\bot SO \\ & AC\cap SO=O \\ \end{aligned} \right.$ nên $BD\bot \left( SAC \right)$.

b) Gọi $E$ là trung điểm $BC$.

Hình chóp $S.ABCD$ đều nên cạnh bên $SB = SC$. 

Do đó tam giác $SBC$ cân tại $S$ nên trung tuyến $SE\bot BC$.

Tứ giác $ABCD$ là hình vuông nên $AC=BD\Rightarrow OB=OC$. 

Do đó tam giác $OBC$ cân tại $O\Rightarrow $trung tuyến $OE\bot BC$.

Ta có $\left( SBC \right)\cap \left( ABCD \right)=BC$; trong $\left( SBC \right)$ có $SE\bot BC$; trong $\left( ABCD \right)$ có $OE\bot BC$.

Do đó góc giữa hai mặt phẳng $\left( SBC \right)$ và $\left( ABCD \right)$ là góc giữa hai đường thẳng $SE$ và $OE$.

Tam giác $SOE$ vuông tại $O$ ( do $SO\bot \left( ABCD \right)$) nên góc giữa hai đường thẳng  $SE$ và $OE$ là $\widehat{SEO}$.

Tam giác $OBC$ vuông tại $O$ ( do $AC\bot BD$) nên trung tuyến $OE=\dfrac{BC}{2}=\dfrac{2a}{2}=a$.

Vậy $\tan \left( \widehat{(SBC),( ABCD)} \right)=\tan \left( \widehat{SE,OE} \right)=\tan \widehat{SEO}=\dfrac{SO}{OE}=\dfrac{a\sqrt{6}}{a}=\sqrt{6}$.

c) Vì $AB$ // $CD$  $\Rightarrow AB$ // $\left( SCD \right)$ $\Rightarrow d\left( AB,SC \right)=d\left( AB,\left( SCD \right) \right)=d\left( A,\left( SCD \right) \right)$.

Gọi $I$ là trung điểm  $CD$. Kẻ ${OJ}\bot SI$, $\left( J\in SI \right)$.

Vì tam giác $OCD$ cân tại $O$ nên trung tuyến $OI\bot CD$.

Vì $\left\{ \begin{aligned} & CD\bot SO \\ & CD\bot OI \\ & SO\cap OI=O \\ \end{aligned} \right.$  nên $CD\bot \left( SOI \right)$$\Rightarrow CD\bot {OJ}$.

Vì $\left\{ \begin{aligned} & {OJ}\bot SI \\ & {OJ}\bot CD \\ & SI\cap CD=I \\ \end{aligned} \right.$ nên ${OJ}\bot \left( SCD \right)\Rightarrow d\left( O,\left( SCD \right) \right)={OJ}$.

Tam giác $OCD$ vuông tại $O$ ( do $AC\bot BD$) nên trung tuyến $OI=\dfrac{CD}{2}=\dfrac{2a}{2}=a$.

Xét tam giác $SOI$ vuông tại $O$ có đường cao $OJ$, ta có: $\dfrac{1}{{O}{{{J}}^{2}}}=\dfrac{1}{S{{O}^{2}}}+\dfrac{1}{O{{I}^{2}}}=\dfrac{1}{{{\left( a\sqrt{6} \right)}^{2}}}+\dfrac{1}{{{a}^{2}}}=\dfrac{7}{6{{a}^{2}}}$

$\Rightarrow {O}{{{J}}^{2}}=\dfrac{6{{a}^{2}}}{7}\Rightarrow {OJ}=\dfrac{\sqrt{42}a}{7}$.

Dễ thấy: $AO\cap \left( SCD \right)=C$, nên ta có $\dfrac{d\left( A,\left( SCD \right) \right)}{d\left( O,\left( SCD \right) \right)}=\dfrac{AC}{OC}=2$

$\Rightarrow d\left( A,\left( SCD \right) \right)=2.d\left( O,\left( SCD \right) \right)=2.{OJ}=2.\dfrac{\sqrt{42}a}{7}=\dfrac{2\sqrt{42}a}{7}$.

Vậy $d\left( AB,SC \right)=d\left( A,\left( SCD \right) \right)=\dfrac{2\sqrt{42}a}{7}$.

Hướng dẫn giải:

Xét hàm số $f\left( x \right)=m{{\left( x+1 \right)}^{2}}{{\left( x-2 \right)}^{3}}+\left( x+2 \right)\left( x-3 \right)$ xác định và liên tục trên $\mathbb{R}$

$\Rightarrow f\left( x \right)$ xác định và liên tục trên $\left[ -2;3 \right]$.

Ta có: $\left\{ \begin{aligned} & f\left( -2 \right)=-64m \\ & f\left( 3 \right)=16m \\ \end{aligned} \right.\Rightarrow f\left( -2 \right).f\left( 3 \right)=-1024{{m}^{2}}$.

+ Với $m=0\Rightarrow f\left( -2 \right)=f\left( 3 \right)=0$

$\Rightarrow$ Phương trình $f\left( x \right)=0$ có nghiệm $x=-2,$ $x=3.$

+ Với $m\ne 0\Rightarrow f\left( -2 \right).f\left( 3 \right)<0$

$\Rightarrow $ Phương trình $f\left( x \right)=0$ có ít nhất một nghiệm thuộc $\left( -2;3 \right)$.

Vậy phương trình $f\left( x \right)=0$ luôn có nghiệm với mọi tham số $m.$