Bài học cùng chủ đề
- Một số dấu hiệu nhận biết tứ giác nội tiếp
- Chứng minh tứ giác nội tiếp (Phần 1)
- Chứng minh tứ giác nội tiếp (Phần 2)
- Tứ giác nội tiếp
- Tứ giác nội tiếp
- Phương pháp: Chứng minh tổng hai góc đối bằng 180 độ
- Phương pháp: Chứng minh hai đỉnh kề nhau cùng nhìn cạnh chứa hai điểm còn lại hai góc bằng nhau
- Phương pháp: Chứng minh góc ngoài tại một đỉnh bằng góc trong của đỉnh đối diện
- Chứng minh đẳng thức tích các đoạn thẳng
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Phương pháp: Chứng minh hai đỉnh kề nhau cùng nhìn cạnh chứa hai điểm còn lại hai góc bằng nhau SVIP
Cho tam giác $ABC$ có ba góc nhọn nội tiếp đường tròn tâm $O$ $(AB < AC)$. Hai tiếp tuyến tại $B$ và $C$ cắt nhau tại $M$. $AM$ cắt đường tròn $(O)$ tại điểm thứ hai $D$. Gọi $E$ là trung điểm đoạn $AD$. Chứng minh $OEBM$ là tứ giác nội tiếp.
Hướng dẫn giải:
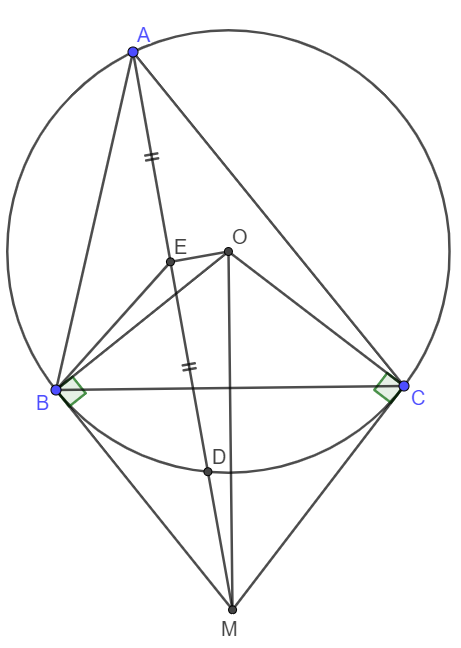
Do BM là tiếp tuyến của đường tròn nên \(\widehat{OBM}=90^o\)
Xét đường tròn (O) có AD là một dây cung. Lại có E là trung điểm AD nên theo tính chất của đường kính và dây cung, ta có \(OE\perp AD\) hay \(\widehat{OEM}=90^o\).
Xét tứ giác OEBM có \(\widehat{OBM}=\widehat{OEM}=90^o\), chúng lại là hai góc kề nhau nên OEBM là tứ giác nội tiếp.
Cho tam giác $ABC$ có ba góc đều nhọn nội tiếp đường tròn tâm $O$, hai đường cao $BD$ và $CE$. Chứng minh tứ giác $BCDE$ nội tiếp được trong một đường tròn.
Hướng dẫn giải:
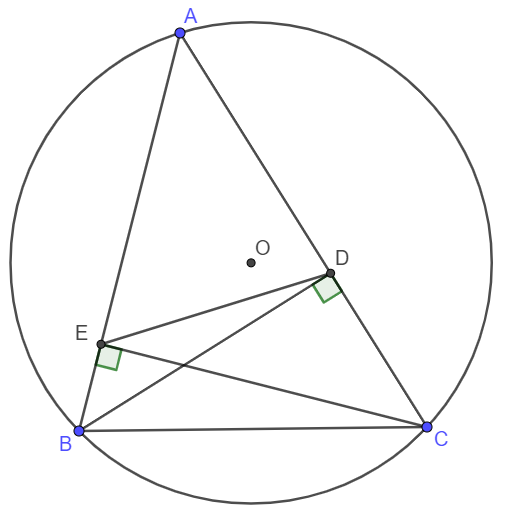
Do BD và CE là các đường cao nên \(\widehat{BEC}=\widehat{BDC}=90^o\)
Xét tứ giác BCDE có \(\widehat{BEC}=\widehat{BDC}\) nên BCDE là tứ giác nội tiếp.
Cho đường tròn tâm $O$ bán kính $R$ và một điểm $A$ nằm ngoài đường tròn. Kẻ một đường thẳng đi qua $A$ và không đi qua $O$, cắt đường tròn tại hai điểm phân biệt $M$, $N$ ($M$ nằm giữa $A$ và $N$). Từ $A$ vẽ hai tiếp tuyến $AB$ và $AC$ với $(O)$ ($B$, $C$ là hai tiếp điểm). Đường thẳng $BC$ cắt $AO$ tại $H$. Gọi $I$ là trung điểm của $MN$. Đường thẳng $OI$ cắt đường thẳng $BC$ tại $E$. Chứng minh $AHIE$ là tứ giác nội tiếp.
Hướng dẫn giải:
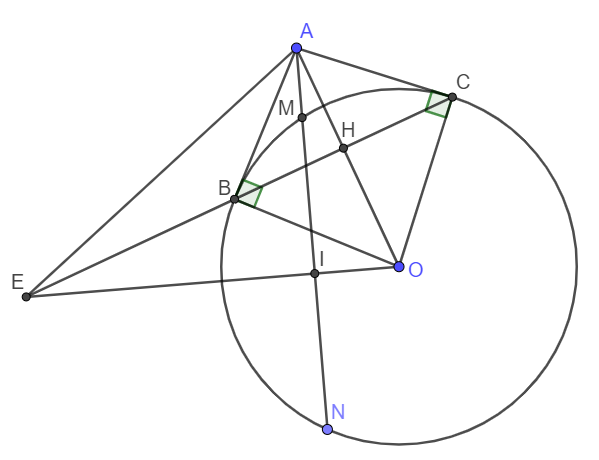
Vì I là trung điểm dây cung MN \(OI\perp MN\Rightarrow\widehat{AIE}=90^o\).
Hai tiếp tuyến của đường tròn (O) tại B và C cắt nhau tại A nên \(OA\perp BC\).
Do tam giác IEA và tam giác HEA là hai tam giác vuông chung cạnh huyền AE nên A, H, I, E cùng nằm trên đường tròn đường kính AE.
Cho tam giác $ABC$ không có góc tù $(AB < AC)$, nội tiếp đường tròn $(O; R)$, ($B$, $C$ cố định, $A$ di động trên cung lớn BC). Các tiếp tuyến tại $B$ và $C$ cắt nhau tại $M$. Từ $M$ kẻ đường thẳng song song với $AB$, đường thẳng này cắt $(O)$ tại $D$ và $E$ ($D$ thuộc cung nhỏ $BC$), cắt $BC$ tại $F$, cắt $AC$ tại $I$. Chứng minh rằng \(\widehat{MBC}=\widehat{BAC}\) . Từ đó suy ra $MBIC$ là tứ giác nội tiếp.
Hướng dẫn giải:
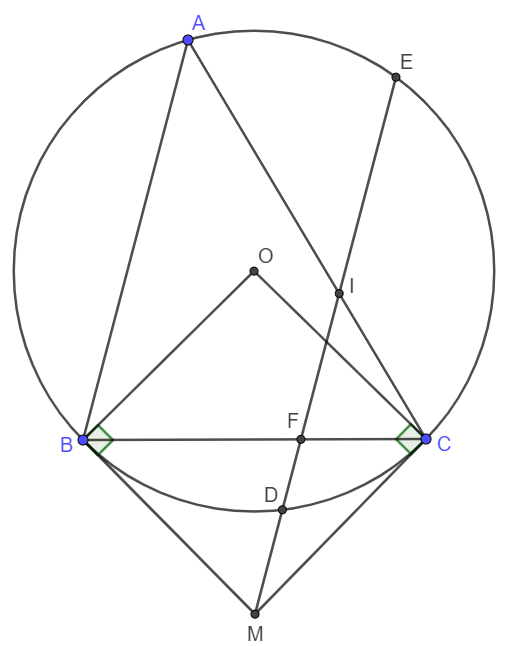
Ta thấy góc \(\widehat{MBC}\) và \(\widehat{BAC}\) cùng chắn cung \(\stackrel\frown{BC}\) nên \(\widehat{MBC}=\widehat{BAC}\) (góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung cùng chắn một cung).
Do MI//AB nên \(\widehat{BAC}=\widehat{MIC}\) (Hai góc đồng vị)
Vậy thì \(\widehat{MBC}=\widehat{MIC}\).
Do đó MBIC là tứ giác nội tiếp.
Cho đường tròn tâm $O$ bán kính $OA$. Điểm $C$ thuộc đoạn thẳng $AO$ ($C$ khác $A$ và $O$). Đường thẳng vuông góc với $AO$ tại $C$ cắt đường tròn $(O)$ tại hai điểm $D$ và $K$. Tiếp tuyến tại $D$ của đường tròn $(O)$ cắt đường thẳng $AO$ tại $E$. Tiếp tuyến tại $A$ của đường tròn $(O)$ cắt đường thẳng $DE$ tại $F$. Gọi $H$ là giao điểm của hai đường thẳng $FO$ và $DK$.
Chứng minh các tứ giác $AFDO$ và $AHOK$ là tứ giác nội tiếp.
Hướng dẫn giải:
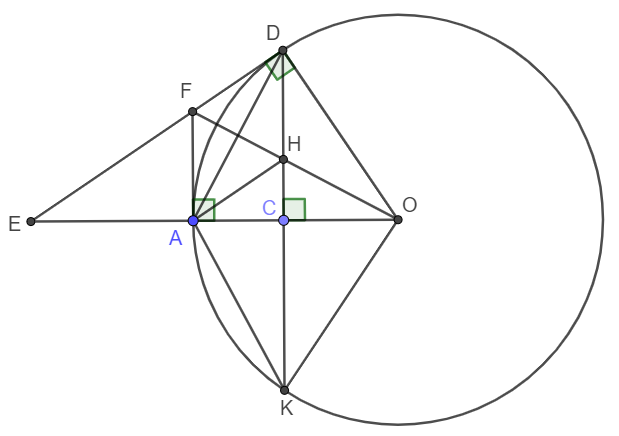
Vì DE là tiếp tuyến của (O) nên DOF là tam giác vuông với cạnh huyền OF. Tương tự, FAO cũng là một tam giác vuông với cạnh huyền OF. Do đó tứ giác AFOD nội tiếp đường tròn đường kính OF.
Vì FA và FD là hai tiếp tuyến cùng xuất phát từ điểm F nên \(OF\perp DA\) , suy ra H là trực tâm tam giác ODA. Do đó \(AH\perp OD\) , suy ra AH // ED.
Vì vậy \(\widehat{HAO}=\widehat{DEO}=\widehat{ODC}=\widehat{DKO}\) nên AHOK nội tiếp.
