Tìm hiểu về SP, GP (tập sau sẽ là coin và xu, quý zị đón xem nha:))
Hôm nay Hà An rảnh rỗi nên sẽ chỉ cho các bạn về SP, GP tại thấy nhiều bạn hỏi quá trời lun à!:))
1. SP là gì?
SP là điểm mà khi bạn trả lời câu hỏi được tick. 1 tick, 1 bấm đúng sẽ tương đương với 1 SP, số bấm đúng càng nhiều thì số SP cũng sẽ càng nhiều.
> Vậy SP nghĩa là gì?
Theo như mình nghĩ và tìm hiểu đôi chút thì SP là viết tắt...
Đọc tiếp
Tìm hiểu về SP, GP (tập sau sẽ là coin và xu, quý zị đón xem nha:))
Hôm nay Hà An rảnh rỗi nên sẽ chỉ cho các bạn về SP, GP tại thấy nhiều bạn hỏi quá trời lun à!:))
1. SP là gì?
SP là điểm mà khi bạn trả lời câu hỏi được tick. 1 tick, 1 bấm đúng sẽ tương đương với 1 SP, số bấm đúng càng nhiều thì số SP cũng sẽ càng nhiều.
> Vậy SP nghĩa là gì?
Theo như mình nghĩ và tìm hiểu đôi chút thì SP là viết tắt của Support tạm dịch là người hỗ trợ. Người hộ trợ ở đây mang ý nghĩa là người khác bấm đúng hỗ trợ bạn có SP đó nha!
> Cách kiếm SP:
Bạn chỉ cần tích cực tham gia hỏi đáp, trả lời chính xác và phù hợp với câu hỏi rồi sẽ được tick nhé. Nhân đây mình xin nói luôn là không phải ai trả lời đúng cũng được tick nhé, nhiều khi cuộc sống có lúc thăng trầm bạn ạ! (riêng mình trầm chứ không có thăng :))
2. GP là gì?
GP giống như SP, chỉ khác chút xíu là thay vì các bạn tick thì các thầy cô hoặc cộng tác viên tick mới có GP. Lưu ý chút là không phải câu nào cũng có được GP đâu nhé!
GP nghĩa là gì?
Theo mình tìm hiểu thì: GP của quý zị (bác sĩ đa khoa, hay bác sĩ gia đình) thường là người đầu tiên quý vị đến gặp nếu có một vấn đề về sức khỏe. Họ điều phối việc chăm sóc sức khỏe cho quý zị và có thể là người chăm sóc trong suốt cuộc đời quý zị.
Còn trong OLM thì nó mang nghĩa là bác sĩ bấm tick, chỉ có những người có chức vụ cao mới có thể cho bạn GP.
> Cách kiếm GP:
Cũng giống như SP nhưng ở GP, chúng ta phải trả lời không những tuyệt đối 100% mà còn phải phù hợp với cách trình bày của khối lớp người hỏi. Ngoài ra thì cũng có những mini games do các thầy cô tổ chức được thưởng GP đó bạn!!!
Lưu ý SP và GP chỉ mang tính chất phân cấp bậc xíu xiu, ai nhiều thì được làm chiến binh nè, CTV (cộng tác viên) nè, mà không có cũng chả sao. Mật bí cho mọi người là không phải thầy cô nào cũng nhiều SP và GP đâu nhé! (cô Thương Hoài đỉnh nhất!)
Pai pai các bạn, chúc các bạn có thật nhiều SP và GP, cảm ơn vì đã đọc bài này. Hy vọng bài viết này bổ ích cho các bạn (mỏi tay mà hong ai đọc chắc tui chớt)! PP❤

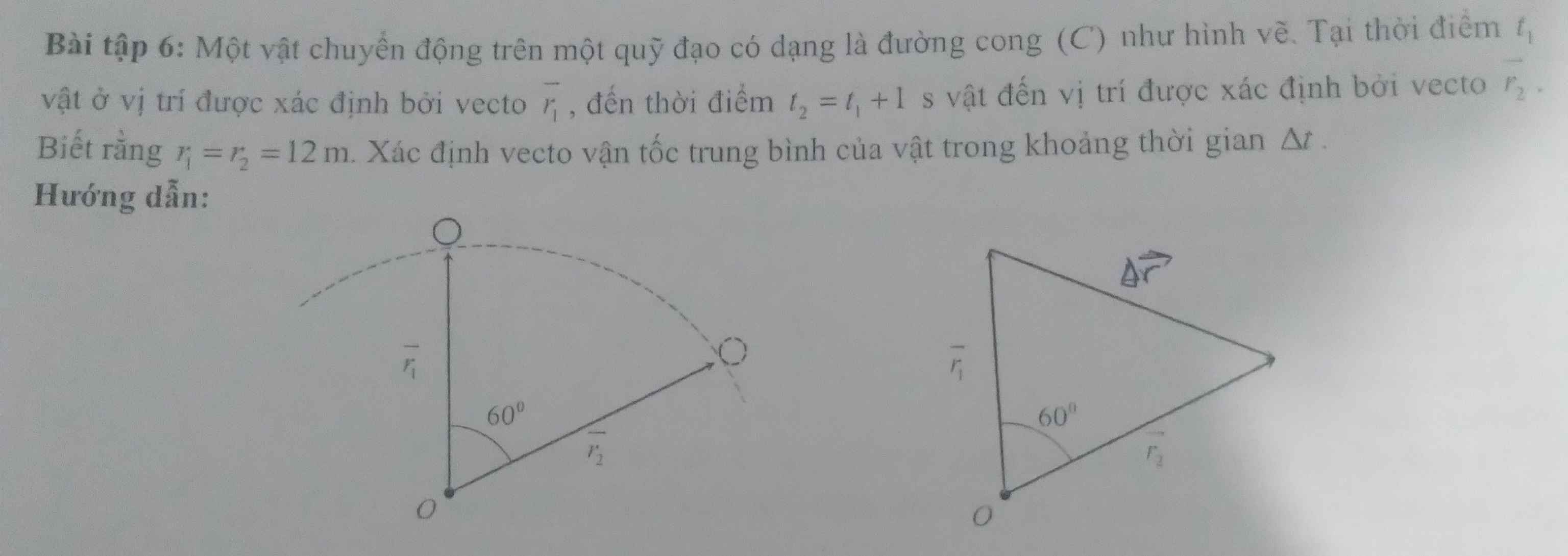

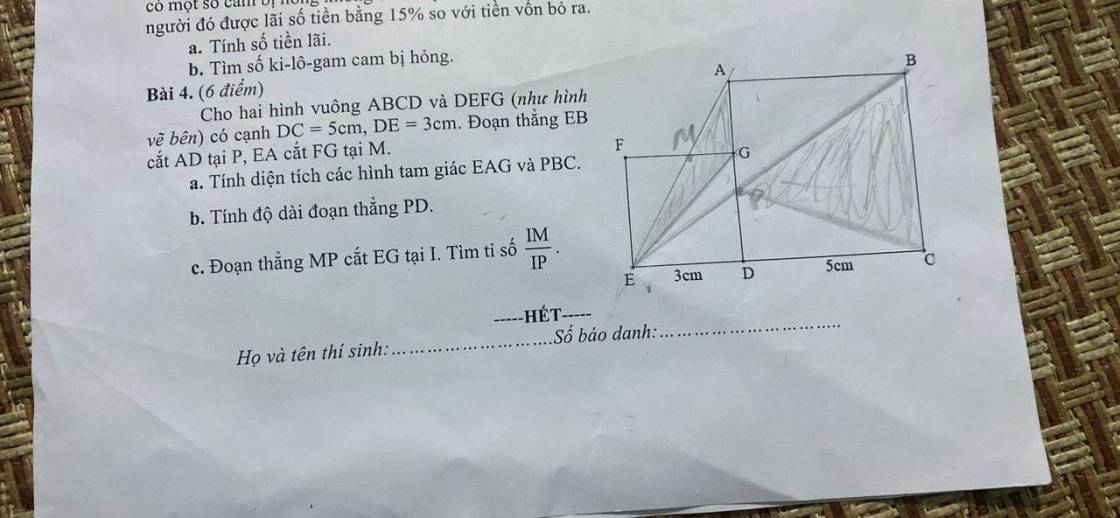
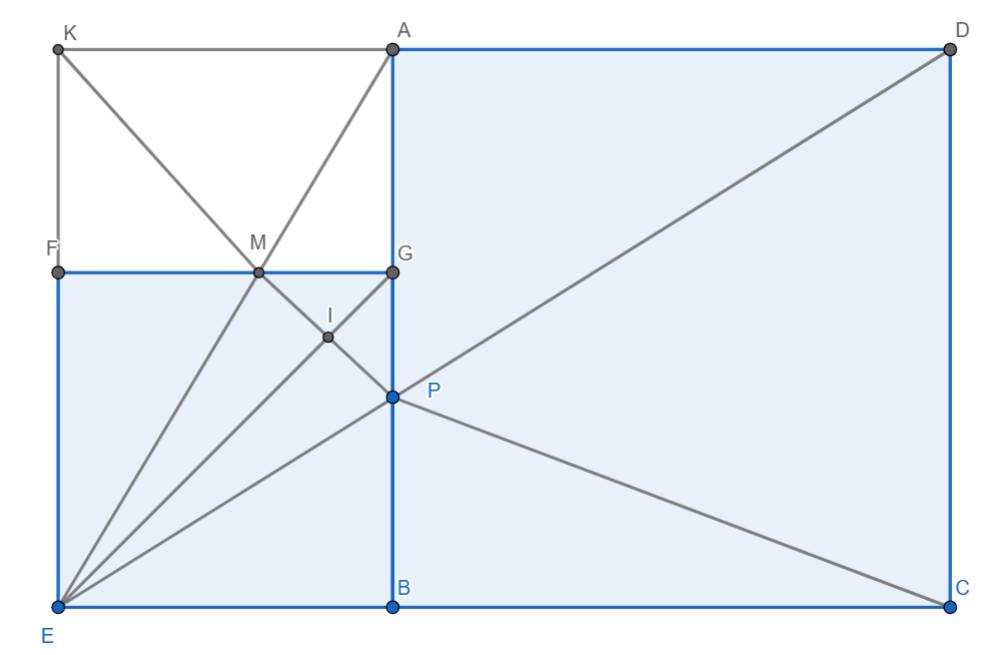
 ai chỉ em với cần gấp lắm cảm ơn
ai chỉ em với cần gấp lắm cảm ơn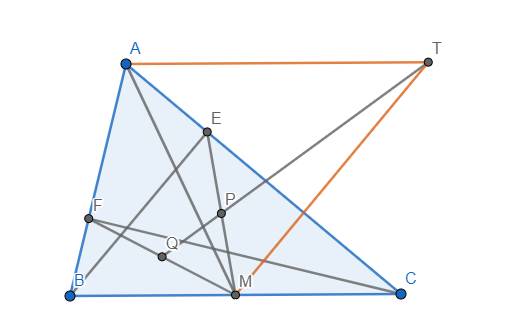
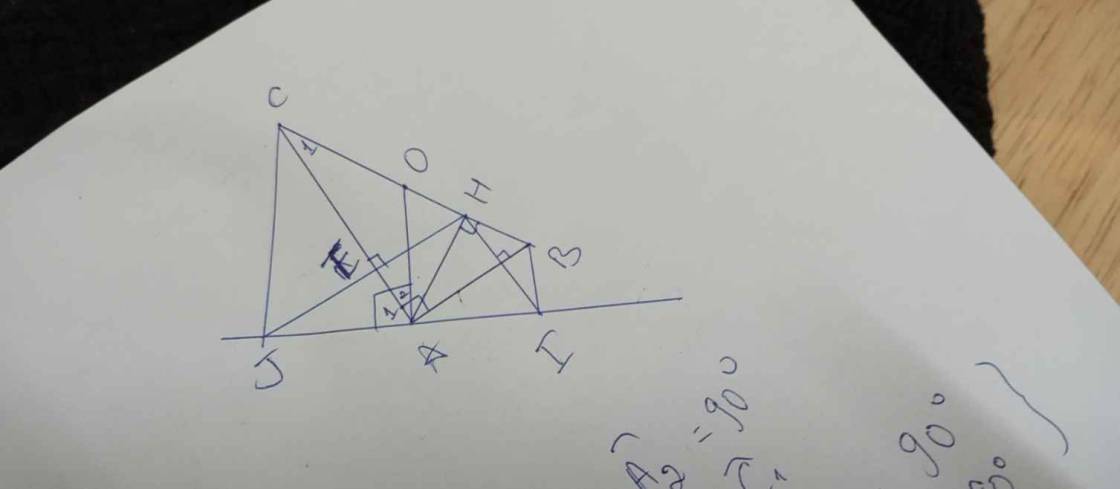
khó quá
Khó thì để cho người khác còn làm !