Qua C dựng đường thẳng t song song với By

⇒ Ct //A\(x\) Vì trong cùng một đường thẳng nếu  hai đường thẳng cùng song song với đường thẳng thứ ba thì song song với nhau.

\(\widehat{ACt}\) + \(\widehat{CAx}\) = 180⁰ (hai góc trong cùng phía)

⇒ \(\widehat{ACt}\) = 180⁰ - 140⁰ = 40⁰

\(\widehat{yBC}\) =  \(\widehat{BCt}\) = 20⁰ (hai góc se trong)

mặt khác ta có: \(\widehat{ACB}\) =  \(\widehat{ACt}\)  + \(\widehat{BCt}\)

               ⇒ \(\widehat{ACB}\) = 40⁰ + 20⁰ 

                   \(\widehat{ACB}\) = 60⁰

Cô ơi cho em hỏi tại sao mình phải chứng minh Ct //Ax

Lời giải:
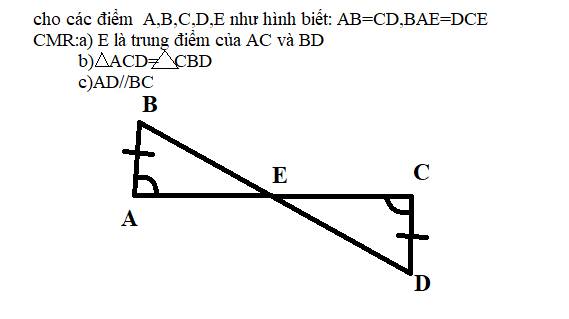
a.

Ta thấy $\widehat{BAE}=\widehat{DCE}$ mà 2 góc này ở vị trí so le trong nên $AB\parallel CD$

$\Rightarrow \widehat{ABE}=\widehat{EDC}$ (so le trong)

Xét tam giác $ABE$ và $CDE$ có:

$AB=CD$

$\widehat{BAE}=\widehat{DCE}$ (gt)

$\widehat{ABE}=\widehat{CDE}$ (cmt) 

$\Rightarrow \triangle ABE=\triangle CDE$ (g.c.g)

$\Rightarrow AE=CE; BE=DE$ nên $E$ là trung điểm $AC, BD$

b. Hai tam giác này không bằng nhau.

c. Xét tam giác $ACD$ và $CAB$ có:
$AC$ chung

$CD=AB$

$\widehat{ACD}=\widehat{CAB}$ 

$\Rightarrow \triangle ACD=\triangle CAB$ (c.g.c)

$\Rightarrow \widehat{CAD}=\widehat{ACB}$

Mà 2 góc này ở vị trí so le trong nên $AD\parallel BC$

Lời giải:

$2x^2+2y^2=5xy$

$\Leftrightarrow 2x^2+2y^2-5xy=0$

$\Leftrightarrow (2x^2-4xy)-(xy-2y^2)=0$

$\Leftrightarrow 2x(x-2y)-y(x-2y)=0$

$\Leftrightarrow (x-2y)(2x-y)=0$

$\Leftrightarrow x=2y$ hoặc $2x=y$

Do $0< x< y$ nên $2x=y$

Khi đó: $E=\frac{x+y}{x-y}=\frac{x+2x}{x-2x}=\frac{3x}{-x}=-3$

Lời giải:

a. $x(\frac{4}{5}x-1)(0,1x-10)=0$

$\Rightarrow x=0$ hoặc $\frac{4}{5}x-1=0$ hoặc $0,1x-10=0$

Nếu $\frac{4}{5}x-1=0$

$\Rightarrow x=1: \frac{4}{5}=\frac{5}{4}$

Nếu $0,1x-10=0$

$\Rightarrow x=10:0,1=100$

Vậy $x=0; \frac{5}{4}; 100$

b.

$(\frac{1}{4}x-1)-(\frac{5}{6}x+2)-(1-\frac{5}{8}x)=0$

$(\frac{1}{4}x-\frac{5}{6}x+\frac{5}{8}x)-(1+2+1)=0$

$\frac{1}{24}x-4=0$

$x=4: \frac{1}{24}=96$

Ta có: \(\dfrac{x+2y-z}{z}=\dfrac{y+2z-x}{x}=\dfrac{z+2x-y}{y}\left(x,y,z\ne0\right)\)

Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:

\(\dfrac{x+2y-z}{z}=\dfrac{y+2z-x}{x}=\dfrac{z+2x-y}{y}\)

\(=\dfrac{x+2y-z+y+2z-x+z+2x-y}{z+x+y}\)

\(=\dfrac{2x+2y+2z}{x+y+z}=\dfrac{2\left(x+y+z\right)}{x+y+z}=2\)

\(\Rightarrow\dfrac{x+2y-z}{z}=\dfrac{y+2z-x}{x}=\dfrac{z+2x-y}{y}=2\)

\(\Rightarrow\dfrac{x+2y}{z}-1=\dfrac{y+2z}{x}-1=\dfrac{z+2x}{y}-1=2\)

\(\Rightarrow\dfrac{x+2y}{z}=\dfrac{y+2z}{x}=\dfrac{z+2x}{y}=3\)

\(\Rightarrow\dfrac{x+2y}{z}\cdot\dfrac{y+2z}{x}\cdot\dfrac{z+2x}{y}=3\cdot3\cdot3\)

\(\Rightarrow\dfrac{x+2y}{y}\cdot\dfrac{y+2z}{z}\cdot\dfrac{z+2x}{x}=27\)

\(\Rightarrow\left(\dfrac{x}{y}+2\right)\left(\dfrac{y}{z}+2\right)\left(\dfrac{z}{x}+2\right)=27\)

hay \(P=27\)

Vậy: ...

Thanks (´▽`ʃ♡ƪ)

Lời giải:
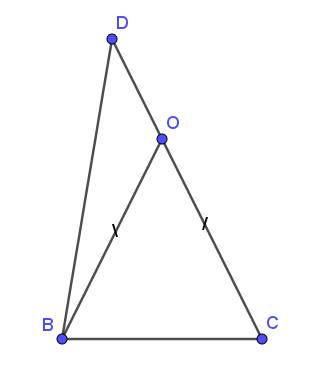
Xét tam giác $OBD$, áp dụng BĐT tam giác thì:

$DB< OB+OD$

Mà $OB=OC$ nên: $OB+OD=OC+OD=CD$

$\Rightarrow DB< CD$ (đpcm)

Hình vẽ:

Lời giải:
a. Ta thấy: $AB\perp BC, CD\perp BC$

$\Rightarrow AB\parallel CD$

$BC\perp CD; DE\perp CD$

$\Rightarrow BC\parallel DE$

b.$AB\perp BC, BC\parallel DE\Rightarrow AB\perp DE$

Mà $DE\perp EF$

$\Rightarrow AB\parallel EF$

c.

Do $AB\parallel CD$ nên: 

$\widehat{AIC}+\widehat{IAB}=180^0$ (2 góc trong cùng phía)

$\Rightarrow \widehat{AIC}=180^0-\widehat{IAB}=180^0-50^0=130^0$