\(\dfrac{3}{2}+\dfrac{19}{6}+\dfrac{61}{12}+...+\dfrac{463}{42}\)

\(=1+3+5+...+11+\left(\dfrac{1}{2}+\dfrac{1}{6}+\dfrac{1}{12}+...+\dfrac{1}{42}\right)\)

Ta đặt biểu thức: 1 + 3 + 5 + ... + 11 = A

                             \(\dfrac{1}{2}+\dfrac{1}{6}+\dfrac{1}{12}+...+\dfrac{1}{42}\) = B

A = (11 + 1) x 6 : 2 = 36

B = Không rõ quy luật.

a) \(5\dfrac{1}{3}:\left(\dfrac{5}{4}-x\right)=0,8\\ \Rightarrow\dfrac{5}{4}-x=5\dfrac{1}{3}:0,8\\ \Rightarrow\dfrac{5}{4}-x=\dfrac{16}{3}:\dfrac{4}{5}\\ \Rightarrow\dfrac{5}{4}-x=\dfrac{16}{3}\times\dfrac{5}{4}\\ \Rightarrow\dfrac{5}{4}-x=\dfrac{20}{3}\\ \Rightarrow x=\dfrac{5}{4}-\dfrac{20}{3}\\ \Rightarrow x=-\dfrac{65}{12}\)

b) \(\dfrac{3}{10}x-2\dfrac{1}{3}=\dfrac{-28}{5}:\dfrac{2}{15}\\ \Rightarrow\dfrac{3}{10}x-\dfrac{7}{3}=\dfrac{-28}{5}\times\dfrac{15}{2}\\ \Rightarrow\dfrac{3}{10}x-\dfrac{7}{3}=-42\\ \Rightarrow\dfrac{3}{10}x=-42+\dfrac{7}{3}\\ \Rightarrow\dfrac{3}{10}x=\dfrac{-119}{3}\\ \Rightarrow x=\dfrac{-119}{3}:\dfrac{3}{10}\\ \Rightarrow x=-\dfrac{1190}{9}\)

a) 

\(5\dfrac{1}{3}:\left(\dfrac{5}{4}-x\right)=0,8\\ \Rightarrow\dfrac{16}{3}:\left(\dfrac{5}{4}-x\right)=\dfrac{4}{5}\\ \Rightarrow\dfrac{5}{4}-x=\dfrac{16}{3}:\dfrac{4}{5}\\ \Rightarrow\dfrac{5}{4}-x=\dfrac{20}{3}\\ \Rightarrow x=\dfrac{5}{4}-\dfrac{20}{3}\\ \Rightarrow x=\dfrac{-65}{12}\)

b) 

\(\dfrac{3}{10}x-2\dfrac{1}{3}=\dfrac{-28}{5}:\dfrac{2}{15}\\ \Rightarrow\dfrac{3}{10}x-\dfrac{7}{3}=\dfrac{-28}{5}\cdot\dfrac{15}{2}\\ \Rightarrow\dfrac{3}{10}x-\dfrac{7}{3}=-42\\ \Rightarrow\dfrac{3}{10}x=-42+\dfrac{7}{3}\\ \Rightarrow\dfrac{3}{10}x=-\dfrac{119}{3}\\ \Rightarrow x=\dfrac{-119}{3}:\dfrac{3}{10}\\ =-\dfrac{1190}{9}\)

AA + BB = CBC

11 x (A + B) = CBC

⇒ B = C x 2

Ta xét các trường hợp:

CBC = 121₁ = 242₂ = 363₃ = 484₄

- Nếu CBC = 121 thì B = 2;  A = 9 và C = 1 (chọn)

Với các trường hợp khác, do đều được tạo bởi các số quá lớn dẫn đến A là số có 2 chữ số nên chỉ có 1 trường hợp nêu trên.

         Giải:

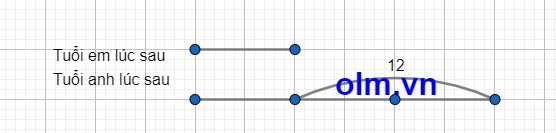
Hiện nay anh hơn em số tuổi là: 16 - 4 = 12 (tuổi)

Dù trước hay sau bao nhiêu năm nữa thì tuổi anh vẫn hơn tuổi emlaf 12 tuổi.

Theo bài ra ta có sơ đồ:

Theo sơ đồ ta có:

Tuổi anh lúc sau là: 12 : (3 - 1) x 3 = 18 (tuổi)

Tuổi anh sẽ gấp tuổi em 3 lần sau số năm là:

  18  -  16  = 2 (năm)

Đáp số: 2 năm

\(\dfrac{-9}{11}< \dfrac{7}{a}< \dfrac{-9}{13}\\ \Rightarrow\dfrac{63}{-77}< \dfrac{63}{9a}< \dfrac{63}{-91}\\ \Rightarrow-77>9a>-91\)

Với \(a\inℤ\Rightarrow9a⋮9\)

Do đó \(9a\in\left\{-81;-90\right\}\)

\(\Rightarrow a\in\left\{-9;-10\right\}\)

Vậy số hữu tỉ thỏa mãn là: \(\dfrac{7}{-9};\dfrac{7}{-10}\)

\(D=1-\dfrac{2}{5\cdot10}-\dfrac{2}{10\cdot15}-\dfrac{2}{15\cdot20}-...-\dfrac{2}{2020\cdot2025}\)

\(D=1-\left(\dfrac{2}{5\cdot10}+\dfrac{2}{10\cdot15}+\dfrac{2}{15\cdot20}+...+\dfrac{2}{2020\cdot2025}\right)\)

Đặt \(A=\dfrac{2}{5\cdot10}+\dfrac{2}{10\cdot15}+\dfrac{2}{15\cdot20}+...+\dfrac{2}{2020\cdot2025}\)

\(A=\dfrac{2}{5}\cdot\left(\dfrac{1}{5}-\dfrac{1}{10}\right)+\dfrac{2}{5}\cdot\left(\dfrac{1}{10}-\dfrac{1}{15}\right)+\dfrac{2}{5}\cdot\left(\dfrac{1}{15}-\dfrac{1}{20}\right)+...+\dfrac{2}{5}\cdot\left(\dfrac{1}{2020}-\dfrac{1}{2025}\right)\)

\(A=\dfrac{2}{5}\cdot\left(\dfrac{1}{5}-\dfrac{1}{10}+\dfrac{1}{10}-\dfrac{1}{15}+\dfrac{1}{15}-\dfrac{1}{20}+...+\dfrac{1}{2020}-\dfrac{1}{2025}\right)\)

\(A=\dfrac{2}{5}\cdot\left(\dfrac{1}{5}-\dfrac{1}{2025}\right)\)

\(A=\dfrac{2}{5}\cdot\dfrac{404}{2025}\)

\(A=\dfrac{808}{10125}\)

Thay vào D được:

\(D=1-\dfrac{808}{10125}\)

\(D=\dfrac{9317}{10125}\)

Vậy \(D=\dfrac{9317}{10125}\)

7 hoặc -7

\(x^2\) = 49

\(x^2\) = 7²

|\(x\)| = 7

\(\left[{}\begin{matrix}x=-7\\x=7\end{matrix}\right.\)

Vậy \(x\) \(\in\) {- 7; 7}

Gọi phân số cần tìm có dạng là \(\dfrac{x}{15}\)  \(\left(x\inℤ\right)\)

Theo đề bài ta có:

\(-\dfrac{3}{5}< \dfrac{x}{15}< -\dfrac{1}{6}\)

\(\Rightarrow-\dfrac{18}{30}< \dfrac{2x}{30}< -\dfrac{5}{30}\)

\(\Rightarrow-18< 2x< -5\)

\(\Rightarrow-9< x< -\dfrac{5}{2}\)

\(\Rightarrow x\in\left\{-8,-7,-6,-5,-4,-3\right\}\)

Suy ra các phân số cần tìm là \(-\dfrac{8}{15};-\dfrac{7}{15};-\dfrac{6}{15};-\dfrac{5}{15};-\dfrac{4}{15};-\dfrac{3}{15}\)

Vậy có 6 phân số thỏa mãn đề bài

phân số thoả mãn đề bài có dạng: \(\dfrac{x}{15}\); \(x\) \(\in\) Z

Theo bài ra ta có: 

                \(\dfrac{-3}{5}\) <  \(\dfrac{x}{15}\) <  \(\dfrac{-1}{6}\)

        \(\dfrac{-3\times6}{5\times6}\) <  \(\dfrac{x\times2}{15\times2}\) < \(\dfrac{-1\times5}{6\times5}\)

              \(\dfrac{-18}{30}\) <  \(\dfrac{x\times2}{30}\) < \(\dfrac{-5}{30}\) 

   30 x  \(\dfrac{-18}{30}\) <  \(\dfrac{x\times2}{30}\) < \(\dfrac{-5}{30}\) x 30

             - 18 <  \(x\times\) 2 < - 5 

            - 18 < \(x\) \(\times\) 2 < - 5

            -18 : 2 < \(x\) < - 5 : 2

           - 9 <  \(x\) < - 2\(\dfrac{1}{2}\)

     Vì \(x\in\) Z nên \(x\) \(\in\) {- 8; - 7; - 6; -5; - 4; - 3}

Vậy có 6 phân số thoả mãn yêu cầu đề bài. 

A

3m\(^3\) 204cm\(^3\) = 3000,204dm\(^3\)

Mà 3000,204dm\(^3\) > 30,204dm\(^3\)

Nên 3m\(^3\) 204cm\(^3\) > 30,204dm\(^3\)

Vậy chọn C