
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


ΔABC=ΔDEF
=>\(\widehat{A}=\widehat{D}\)
=>\(\widehat{D}=55^0\)
ΔABC=ΔDEF
=>\(\widehat{B}=\widehat{E}\)
=>\(\widehat{B}=75^0\)
Xét ΔABC có \(\widehat{A}+\widehat{B}+\widehat{C}=180^0\)
=>\(\widehat{C}=180^0-55^0-75^0=50^0\)
=>\(\widehat{F}=\widehat{C}=50^0\)

\(\dfrac{11}{3}+\left|x\right|=\dfrac{9}{4}\)
=>\(\left|x\right|=\dfrac{9}{4}-\dfrac{11}{3}=\dfrac{27}{12}-\dfrac{44}{12}=-\dfrac{17}{12}\)
mà \(\left|x\right|>=0\forall x\)
nên \(x\in\varnothing\)

\(\left(\dfrac{1}{2}\right)^{x+2}=16^{4-2x}\)
=>\(2^{-x-2}=2^{4\left(4-2x\right)}\)
=>-x-2=4*(4-2x)
=>-x-2=16-8x
=>-x+8x=16+2
=>7x=18
=>\(x=\dfrac{18}{7}\)

Bài 2:
a) \(\dfrac{-7}{-13}=\dfrac{7}{13}\) là số hưu tỉ dương
b) \(\dfrac{2}{-17}=-\dfrac{2}{17}\) là số hưu tỉ âm
c) \(-\dfrac{-6}{5}=\dfrac{6}{5}\) là số hưu tỉ dương
Bài 3:
a) \(-2\dfrac{1}{4}=-\left(2+\dfrac{1}{4}\right)=-\dfrac{9}{4}\)
b) \(6\dfrac{2}{3}=6+\dfrac{2}{3}=\dfrac{20}{3}\)
c) \(-3\dfrac{1}{4}=-\left(3+\dfrac{1}{4}\right)=-\dfrac{13}{4}\)

Bài 1:
\(3^{39}< 3^{40}=\left(3^4\right)^{10}=81^{10}\)
\(11^{21}>11^{20}=121^{10}\)
mà 121>81
nên \(11^{21}>3^{39}\)
Bài 2:
\(5^{27}=\left(5^3\right)^9=125^9;2^{63}=\left(2^7\right)^9=128^9\)
mà 125<128
nên \(5^{27}< 2^{63}\)
\(2^{63}=\left(2^9\right)^7=512^7;5^{28}=\left(5^4\right)^7=625^7\)
mà 512<625
nên \(2^{63}< 5^{28}\)
Do đó: \(5^{27}< 2^{63}< 5^{28}\)

sửa đề chia hết 31 nhé
\(S=5+5^2+5^3+...+5^{2019}=5\left(1+5+5^2+5^3\right)+...+5^{2016}\left(1+5+5^2+5^3\right)\)
\(=31\left(5+...+5^{2016}\right)⋮31\)
Vậy ta có đpcm

a: Xét ΔAPE vuông tại P và ΔAPH vuông tại P có
AP chung
PE=PH
Do đó: ΔAPE=ΔAPH
Xét ΔAQH vuông tại Q và ΔAQF vuông tại Q có
AQ chung
QH=QF
Do đó; ΔAQH=ΔAQF
b: ΔAPE=ΔAPH
=>\(\widehat{PAE}=\widehat{PAH}\)
=>AP là phân giác của góc HAE
ΔAQH=ΔAQF
=>\(\widehat{QAH}=\widehat{QAF}\)
=>AQ là phân giác của góc HAF
\(\widehat{EAF}=\widehat{EAH}+\widehat{FAH}\)
\(=2\widehat{QAH}+2\cdot\widehat{PAH}=2\cdot\left(\widehat{QAH}+\widehat{PAH}\right)\)
\(=2\cdot\widehat{QAP}=180^0\)
=>E,A,F thẳng hàng

Bài 6: Oz là phân giác của góc xOy
=>\(\widehat{xOz}=\dfrac{\widehat{xOy}}{2}=\dfrac{142^0}{2}=71^0\)
Ta có: \(\widehat{xOz}+\widehat{x'Oz}=180^0\)(hai góc kề bù)
=>\(\widehat{x'Oz}+71^0=180^0\)
=>\(\widehat{x'Oz}=109^0\)
Bài 7:
Ta có: Oz là phân giác của góc xOy
=>\(\widehat{xOz}=\widehat{yOz}=\dfrac{\widehat{xOy}}{2}=\dfrac{180^0}{2}=90^0\)
Ot là phân giác của góc xOz
=>\(\widehat{zOt}=\dfrac{\widehat{xOz}}{2}=\dfrac{90^0}{2}=45^0\)
Ov là phân giác của góc yOz
=>\(\widehat{vOz}=\dfrac{90^0}{2}=45^0\)
\(\widehat{vOt}=\widehat{zOv}+\widehat{zOt}=45^0+45^0=90^0\)

b: \(\dfrac{4^5+4^5+4^5+4^5}{3^5+3^5+3^5}\cdot\dfrac{6^5+6^5+6^5+6^5+6^5+6^5}{2^5+2^5}=8^x\)
=>\(8^x=\dfrac{4\cdot4^5}{3\cdot3^5}\cdot\dfrac{6\cdot6^5}{2\cdot2^5}\)
=>\(8^x=\dfrac{4^6}{2^6}\cdot\dfrac{6^6}{3^6}=2^6\cdot2^6=2^{12}=\left(2^3\right)^4=8^4\)
=>x=4




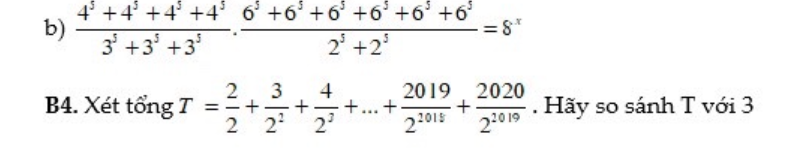
Bài 4: \(8^{10}\cdot125^{10}< =2^n\cdot5^n< =20^{16}\cdot5^{16}\)
=>\(1000^{10}< =10^n< =100^{16}\)
=>\(10^{30}< =10^n< =10^{32}\)
=>30<=n<=32
mà n là số tự nhiên
nên \(n\in\left\{30;31;32\right\}\)
Bài 1:
1: \(3^{-2}\cdot3^4\cdot3^n=3^7\)
=>\(3^n\cdot3^2=3^7\)
=>n+2=7
=>n=7-2=5
2: \(2^{-1}\cdot2^n+4\cdot2^n=9\cdot2^5\)
=>\(2^n\left(\dfrac{1}{2}+4\right)=2^5\cdot9\)
=>\(2^n=9\cdot2^5:\dfrac{9}{2}=2^6\)
=>n=6
Bài 2:
1: \(243>=3^n>=9\)
=>\(3^2< =3^n< =3^5\)
=>2<=n<=5
mà n là số tự nhiên
nên \(n\in\left\{2;3;4;5\right\}\)
2: \(2^{n+3}\cdot2^n=144\)
=>\(2^{2n+3}=144\)
=>\(2n+3=log_2144\)
=>\(2n=log_2144-3\)
=>\(n=\dfrac{log_2144-3}{2}\left(loại\right)\)
Bài 3:
\(10^x:5^y=20^y\)
=>\(10^x=20^y\cdot5^y=100^y=10^{2y}\)
=>x=2y
vậy: \(\left(x;y\right)\in\){(2k;k)|\(k\in N\)}