x^2y^2-4x-4y là số chính phương
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


3) x³ = 343
x³ = 7³
x = 7
4) (7x - 11)³ = 2⁵.5² + 200
(7x - 11)³ = 32.25 + 200
(7x - 11)³ = 800 + 200
(7x - 11)³ = 1000
(7x - 11)³ = 10³
7x - 11 = 10
7x = 10 + 11
7x = 21
x = 21 : 7
x = 3
6) Điều kiện: x 2019
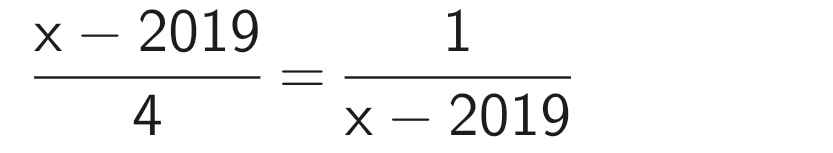
(x - 2019).(x - 2019) = 1.4
(x - 2019)² = 4
(x - 2019)² = 2² hoặc (x - 2019)² = (-2)²
x - 2019 = 2 hoặc x - 2019 = -2
*) x - 2019 = 2
x = 2 + 2019
x = 2021 (nhận)
*) x - 2019 = -2
x = -2 + 2019
x = 2017 (nhận)
Vậy x = 2017; x = 2021

Gọi số gà mái ban đầu là x(con)
(Điều kiện: \(x\in Z^+\))
Số gà trống ban đầu là 0,5x
Số con gà trống lúc sau là 0,5x+72
Số gà trồng sẽ bằng 60% số gà mái nên ta có:
0,5x+72=0,6x
=>-0,1x=-72
=>x=720(nhận)
Số gà trống ban đầu là 720*0,5=360 con
Tổng số con gà ban đầu là 360+720=1080(con)

`E =` {`x ∈ N| x + 8 = 2`}
`=> E =` {`∅`} Vì `x = 2 - 8 = -6 ∉ N`
`F =` {`a ∈ N| a . 0 = 0`}
`=> F =` {`0;1;2;3;4;5;...`.} Vì số tự nhiên nào nhân 0 cũng bằng 0

Do số dầu ở thùng 3 = \(\dfrac{3}{4}\) số dầu ở thừng 1 và 2 nên ta có tổng số phần bằng nhau là: 3 + 4 = 7 (phần)
Số dầu ở thùng 3 là: 84 : 7 x 3 = 36 (l)
Tổng số dầu ở thùng 1 và 2 là: 84 - 36 = 48 (l)
Số dầu thùng 1 là: 48 : (3 + 5) x 3 = 18 (l)
Số dầu thùng 2 là: 48 - 18 = 30 (l)
Đáp số: Thùng 1: 18 l dầu
Thùng 2: 30 l dầu
Thùng 3: 36 l dầu

\(\dfrac{0,4-\dfrac{2}{9}+\dfrac{2}{11}}{1,4-\dfrac{7}{9}+\dfrac{7}{11}}-\dfrac{\dfrac{1}{3}-0,25+\dfrac{1}{7}}{1\dfrac{1}{6}-0,875+\dfrac{1}{2}}\)
= \(\dfrac{\dfrac{2}{5}-\dfrac{2}{9}+\dfrac{2}{11}}{\dfrac{7}{5}-\dfrac{7}{9}+\dfrac{7}{11}}-\dfrac{\dfrac{2}{6}-\dfrac{2}{8}+\dfrac{2}{14}}{\dfrac{7}{6}-\dfrac{7}{8}+\dfrac{7}{14}}\)
= \(\dfrac{2.\left(\dfrac{1}{5}-\dfrac{1}{9}+\dfrac{1}{11}\right)}{7.\left(\dfrac{1}{5}-\dfrac{1}{9}+\dfrac{1}{11}\right)}-\dfrac{2.\left(\dfrac{1}{6}-\dfrac{1}{8}+\dfrac{1}{14}\right)}{7.\left(\dfrac{1}{6}-\dfrac{1}{8}+\dfrac{1}{14}\right)}\)
= \(\dfrac{2}{7}-\dfrac{2}{7}\)
= `0`
\(=\dfrac{2.\left(0,2-\dfrac{1}{7}+\dfrac{1}{11}\right)}{7.\left(0,2-\dfrac{1}{7}+\dfrac{1}{11}\right)}-\dfrac{2.\left(\dfrac{1}{6}-0,125+\dfrac{1}{14}\right)}{7.\left(\dfrac{1}{6}-0,125+\dfrac{1}{14}\right)}\)
\(=\dfrac{2}{7}-\dfrac{2}{7}=0\)

Bài giải
Số sách của thư viện sau 1 năm là :
(1000*20:100)+1000 = 1200 ( sách )
Số sách của thư viện sau 2 năm là :
(1200*20:100)+1200 = 1440 ( sách )
Đáp số : 1440 sách
( DẤU * LÀ DẤU NHÂN NHA :0 )
bài này cũng dễ ấy mà =)

a: \(\left|5-\dfrac{2}{3}x\right|>=0\forall x;\left|\dfrac{2}{3}y-4\right|>=0\forall y\)
Do đó: \(\left|5-\dfrac{2}{3}x\right|+\left|\dfrac{2}{3}y-4\right|>=0\forall x,y\)
Dấu '=' xảy ra khi \(\left\{{}\begin{matrix}5-\dfrac{2}{3}x=0\\\dfrac{2}{3}y-4=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=5:\dfrac{2}{3}=\dfrac{15}{2}\\y=4:\dfrac{2}{3}=6\end{matrix}\right.\)
b: \(\left|\dfrac{2}{3}-\dfrac{1}{2}+\dfrac{3}{4}x\right|>=0\forall x;\left|1,5-\dfrac{3}{4}-\dfrac{3}{2}y\right|>=0\forall y\)
Do đó: \(\left\{{}\begin{matrix}\dfrac{2}{3}-\dfrac{1}{2}+\dfrac{3}{4}x=0\\1,5-\dfrac{3}{4}-\dfrac{3}{2}y=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{3}{4}x=-\dfrac{2}{3}+\dfrac{1}{2}=-\dfrac{1}{6}\\\dfrac{3}{2}y=1,5-\dfrac{3}{4}=\dfrac{3}{2}-\dfrac{3}{4}=\dfrac{3}{4}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=-\dfrac{1}{6}:\dfrac{3}{4}=-\dfrac{1}{6}\cdot\dfrac{4}{3}=\dfrac{-4}{18}=-\dfrac{2}{9}\\y=\dfrac{1}{2}\end{matrix}\right.\)
c: \(\left|x-2020\right|>=0\forall x;\left|y-2021\right|>=0\forall y\)
Do đó: \(\left|x-2020\right|+\left|y-2021\right|>=0\forall x,y\)
Dấu '=' xảy ra khi \(\left\{{}\begin{matrix}x-2020=0\\y-2021=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2020\\y=2021\end{matrix}\right.\)
d: \(\left|x-y\right|>=0\forall x,y\)
\(\left|y+\dfrac{21}{10}\right|>=0\forall y\)
Do đó: \(\left|x-y\right|+\left|y+\dfrac{21}{10}\right|>=0\forall x,y\)
Dấu '=' xảy ra khi \(\left\{{}\begin{matrix}x-y=0\\y+\dfrac{21}{10}=0\end{matrix}\right.\Leftrightarrow x=y=-\dfrac{21}{10}\)

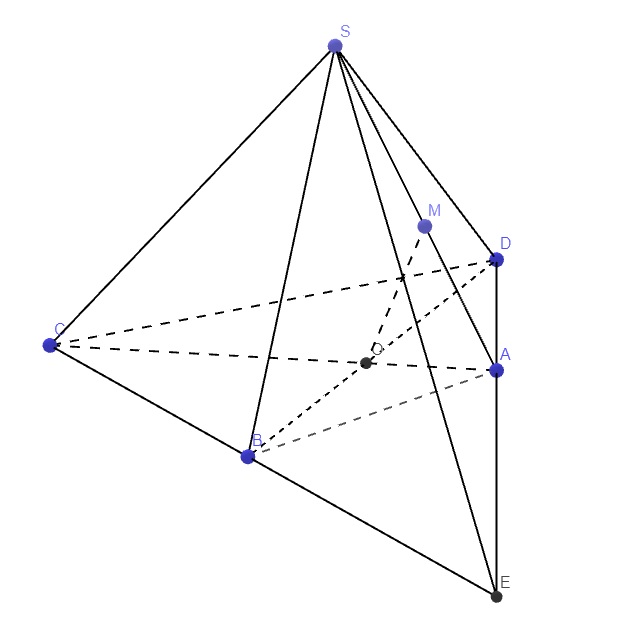
a.
\(S\in\left(SAC\right)\cap\left(SBD\right)\)
Trong mp (ABCD), gọi O là giao điểm AC và BD
\(\left\{{}\begin{matrix}O\in AC\in\left(SAC\right)\\O\in BD\in\left(SBD\right)\end{matrix}\right.\)
\(\Rightarrow O\in\left(SAC\right)\cap\left(SBD\right)\)
\(\Rightarrow SO=\left(SAC\right)\cap\left(SBD\right)\)
b.
\(S\in\left(SAC\right)\cap\left(SBD\right)\)
Trong mp (ABCD), kéo dài AD và BC cắt nhau tại E
\(\left\{{}\begin{matrix}E\in AD\in\left(SAD\right)\\E\in BC\in\left(SBC\right)\end{matrix}\right.\)
\(\Rightarrow E\in\left(SAD\right)\cap\left(SBC\right)\)
\(\Rightarrow SE=\left(SAC\right)\cap\left(SBC\right)\)
c.
\(\left\{{}\begin{matrix}O\in BD\in\left(BDM\right)\\O\in SC\in\left(SAC\right)\end{matrix}\right.\)
\(\Rightarrow O\in\left(BDM\right)\cap\left(SAC\right)\)
\(\left\{{}\begin{matrix}M\in\left(BDM\right)\\M\in SA\in\left(SAC\right)\end{matrix}\right.\)
\(\Rightarrow M\in\left(BDM\right)\cap\left(SAC\right)\)
\(\Rightarrow OM=\left(BDM\right)\cap\left(SAC\right)\)
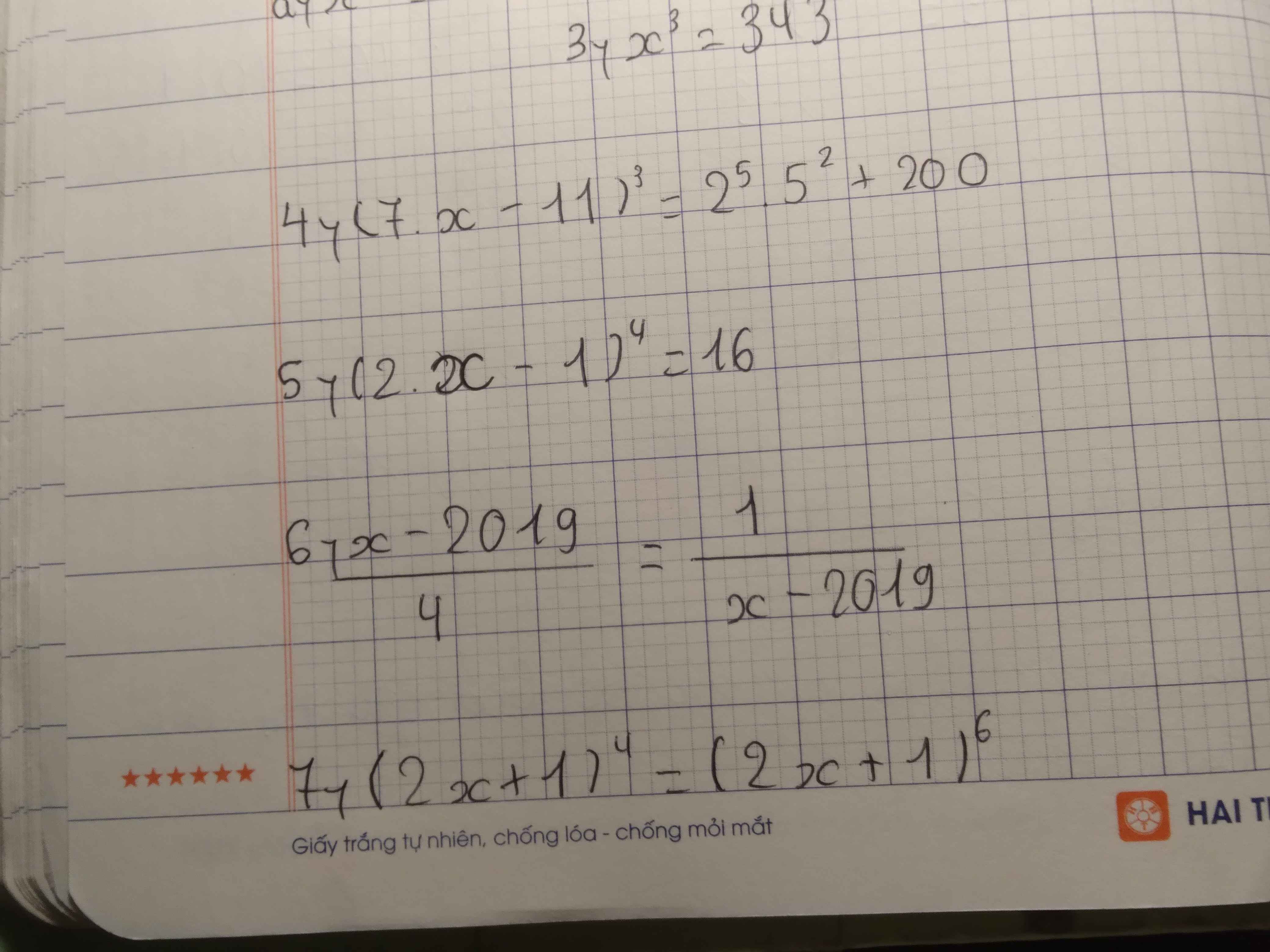
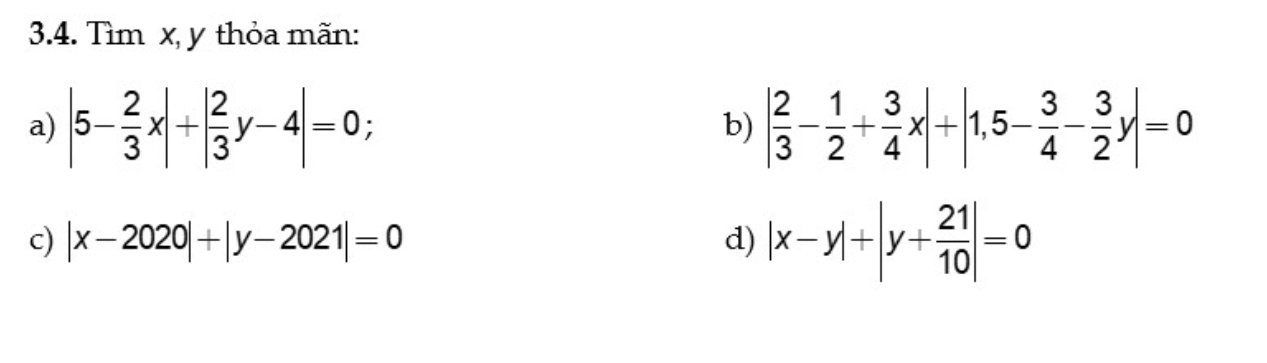
Đề yêu cầu chứng minh hay tìm \(x;y\) vậy em nhỉ?