
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



a: Xét ΔNMH vuông tại M và ΔNKH vuông tại K có
NH chung
NM=NK
Do đó: ΔNMH=ΔNKH
b: Xét ΔHMI vuông tại M và ΔHKP vuông tại K có
HM=HK
\(\widehat{MHI}=\widehat{KHP}\)
Do đó: ΔHMI=ΔHKP
Suy ra: HI=HP
hay ΔHIP cân tại H

Bài 2:
a) \(\dfrac{2}{15}-\dfrac{7}{10}=\dfrac{4}{30}-\dfrac{21}{30}=-\dfrac{17}{30}\)
b) \(\dfrac{-3}{14}+\dfrac{2}{21}=\dfrac{-9}{42}+\dfrac{4}{42}=\dfrac{-5}{42}\)
c) \(\dfrac{-6}{9}+\dfrac{-12}{16}=\dfrac{-96}{144}+\dfrac{-108}{144}=\dfrac{-204}{144}=-\dfrac{17}{12}\)
Bài 3:
a) \(\dfrac{3}{8}+\dfrac{-5}{6}=\dfrac{3}{8}-\dfrac{5}{6}=\dfrac{18}{48}-\dfrac{40}{48}=-\dfrac{22}{48}=-\dfrac{11}{24}\)
b) \(\dfrac{-8}{18}-\dfrac{15}{27}=\dfrac{-24}{54}-\dfrac{30}{54}=\dfrac{-54}{54}=-1\)
c) \(\dfrac{2}{21}-\dfrac{-1}{28}=\dfrac{8}{84}-\dfrac{-3}{84}=\dfrac{11}{84}\)

c. \(\left|\dfrac{8}{4}-\left|x-\dfrac{1}{4}\right|\right|-\dfrac{1}{2}=\dfrac{3}{4}\)
\(\Rightarrow\left[{}\begin{matrix}\left|\dfrac{8}{4}-x+\dfrac{1}{4}\right|-\dfrac{1}{2}=\dfrac{3}{4}\\\left|\dfrac{8}{4}+x-\dfrac{1}{4}\right|-\dfrac{1}{2}=\dfrac{3}{4}\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}\left|\dfrac{9}{4}-x\right|-\dfrac{1}{2}=\dfrac{3}{4}\\\left|\dfrac{7}{4}+x\right|-\dfrac{1}{2}=\dfrac{3}{4}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}\left[{}\begin{matrix}\dfrac{9}{4}-x-\dfrac{1}{2}=\dfrac{3}{4}\\x=\dfrac{9}{4}-\dfrac{1}{2}=\dfrac{3}{4}\end{matrix}\right.\\\left[{}\begin{matrix}\dfrac{7}{4}+x-\dfrac{1}{2}=\dfrac{3}{4}\\-\dfrac{7}{4}-x-\dfrac{1}{2}=\dfrac{3}{4}\end{matrix}\right.\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}\left[{}\begin{matrix}x=1\\x=\dfrac{7}{2}\end{matrix}\right.\\\left[{}\begin{matrix}x=-\dfrac{1}{2}\\x=-3\end{matrix}\right.\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=1\\x=\dfrac{7}{2}\\x=-3\end{matrix}\right.\)
Ở nơi x=9/4-1/2 là x-9/4-1/2 nha
a. -1,5 + 2x = 2,5
<=> 2x = 2,5 + 1,5
<=> 2x = 4
<=> x = 2
b. \(\dfrac{3}{2}\left(x+5\right)-\dfrac{1}{2}=\dfrac{4}{3}\)
<=> \(\dfrac{3}{2}x+\dfrac{15}{2}-\dfrac{1}{2}=\dfrac{4}{3}\)
<=> \(\dfrac{9x}{6}+\dfrac{45}{6}-\dfrac{3}{6}=\dfrac{8}{6}\)
<=> 9x + 45 - 3 = 8
<=> 9x = 8 + 3 - 45
<=> 9x = -34
<=> x = \(\dfrac{-34}{9}\)


Lời giải:
$\frac{5^5}{5^x}=5^{18}$
$5^{5-x}=5^{18}$
$5-x=18$
$x=-13$

b) Ta có: \(\left|2x-1\right|=\left|x+3\right|\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-1=x+3\\2x-1=-x-3\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2x-x=3+1\\2x+x=-3+1\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=4\\x=\dfrac{2}{3}\end{matrix}\right.\)

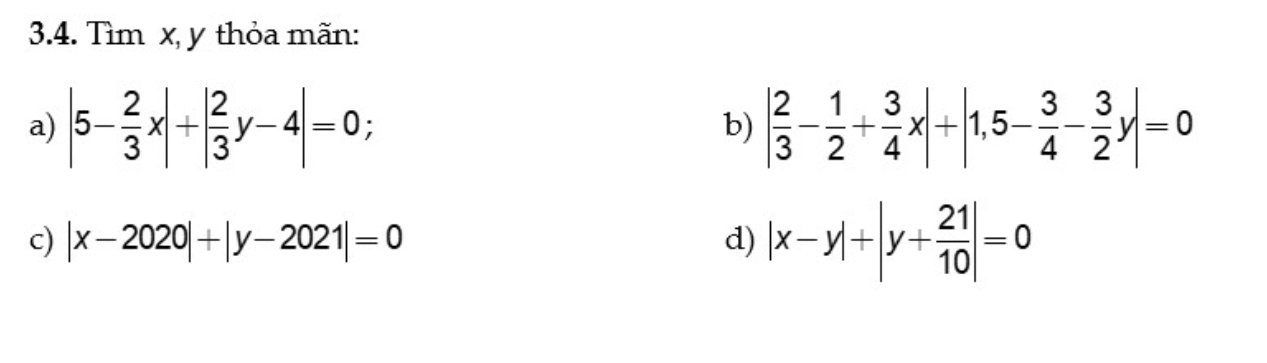


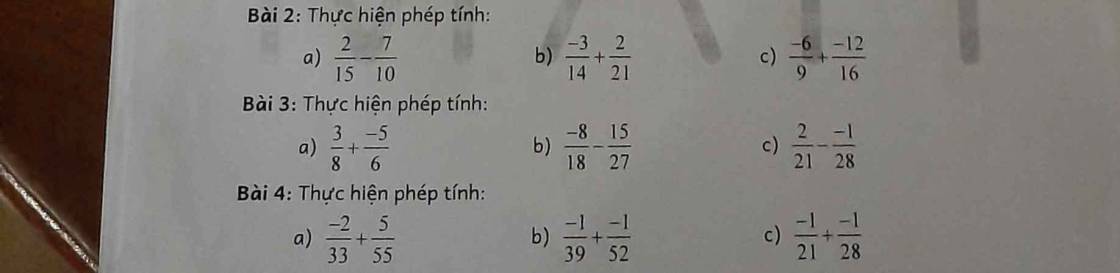


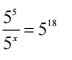

 giúp tui bài 3 gấp lắm
giúp tui bài 3 gấp lắm
a: \(\left|5-\dfrac{2}{3}x\right|>=0\forall x;\left|\dfrac{2}{3}y-4\right|>=0\forall y\)
Do đó: \(\left|5-\dfrac{2}{3}x\right|+\left|\dfrac{2}{3}y-4\right|>=0\forall x,y\)
Dấu '=' xảy ra khi \(\left\{{}\begin{matrix}5-\dfrac{2}{3}x=0\\\dfrac{2}{3}y-4=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=5:\dfrac{2}{3}=\dfrac{15}{2}\\y=4:\dfrac{2}{3}=6\end{matrix}\right.\)
b: \(\left|\dfrac{2}{3}-\dfrac{1}{2}+\dfrac{3}{4}x\right|>=0\forall x;\left|1,5-\dfrac{3}{4}-\dfrac{3}{2}y\right|>=0\forall y\)
Do đó: \(\left\{{}\begin{matrix}\dfrac{2}{3}-\dfrac{1}{2}+\dfrac{3}{4}x=0\\1,5-\dfrac{3}{4}-\dfrac{3}{2}y=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{3}{4}x=-\dfrac{2}{3}+\dfrac{1}{2}=-\dfrac{1}{6}\\\dfrac{3}{2}y=1,5-\dfrac{3}{4}=\dfrac{3}{2}-\dfrac{3}{4}=\dfrac{3}{4}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=-\dfrac{1}{6}:\dfrac{3}{4}=-\dfrac{1}{6}\cdot\dfrac{4}{3}=\dfrac{-4}{18}=-\dfrac{2}{9}\\y=\dfrac{1}{2}\end{matrix}\right.\)
c: \(\left|x-2020\right|>=0\forall x;\left|y-2021\right|>=0\forall y\)
Do đó: \(\left|x-2020\right|+\left|y-2021\right|>=0\forall x,y\)
Dấu '=' xảy ra khi \(\left\{{}\begin{matrix}x-2020=0\\y-2021=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2020\\y=2021\end{matrix}\right.\)
d: \(\left|x-y\right|>=0\forall x,y\)
\(\left|y+\dfrac{21}{10}\right|>=0\forall y\)
Do đó: \(\left|x-y\right|+\left|y+\dfrac{21}{10}\right|>=0\forall x,y\)
Dấu '=' xảy ra khi \(\left\{{}\begin{matrix}x-y=0\\y+\dfrac{21}{10}=0\end{matrix}\right.\Leftrightarrow x=y=-\dfrac{21}{10}\)