a) Ta thấy \(OE=OF\Rightarrow\) O thuộc trung trực của EF.

 Mặt khác, theo tính chất của 2 tiếp tuyến cắt nhau, \(ME=MF\), suy ra M cũng nằm trên trung trực của EF.

 \(\Rightarrow\)OM là trung trực của EF. Mà OM cắt EF tại H nên H là trung điểm EF (đpcm)

b) Ta thấy \(\widehat{OAM}+\widehat{OFM}=90^o+90^o=180^o\)  nên tứ giác OAMF nội tiếp hay 4 điểm O, M, A, F cùng thuộc 1 đường tròn.

c) Vì OM là trung trực EF nên \(OM\perp EF\) tại H \(\Rightarrow\widehat{MHK}=90^o\)

Từ đó dễ thấy tứ giác AMHK nội tiếp \(\Rightarrow OA.OK=OH.OM\)

Mà \(OH.OM=OE^2=R^2\) (hệ thức lượng trong tam giác vuông)

\(\Rightarrow OA.OK=R^2\) (đpcm)

\(\dfrac{\left(2009-x\right)^2+\left(2009-x\right)\left(x-2010\right)+\left(x-2010\right)^2}{\left(2009-x\right)^2-\left(2009-x\right)\left(x-2010\right)+\left(x-2010\right)^2}=\dfrac{19}{49}\left(1\right)\)

\(Đkxđ:x\ne2009;x\ne2010\)

Đặt \(t=x-2010\left(t\ne0\right)\)

\(\Rightarrow2009-x=-\left(t+1\right)\)

\(\left(1\right)\Leftrightarrow\dfrac{\left(t+1\right)^2-\left(t+1\right)t+t^2}{\left(t+1\right)^2+\left(t+1\right)t+t^2}=\dfrac{19}{49}\)

\(\Leftrightarrow\dfrac{t^2+2t+1-t^2-t+t^2}{t^2+2t+1+t^2+t+t^2}=\dfrac{19}{49}\)

\(\Leftrightarrow\dfrac{t^2+t+1}{3t^2+3t+1}=\dfrac{19}{49}\)

\(\Leftrightarrow49t^2+49t+49=57t^2+57t+19\)

\(\Leftrightarrow8t^2+8t-30=0\)

\(\Leftrightarrow4t^2+4t-15=0\)

\(\Leftrightarrow\left(4t^2+4t+1\right)-16=0\)

\(\Leftrightarrow\left(2t+1\right)^2=16=4^2\)

\(\Leftrightarrow\left[{}\begin{matrix}2t+1=4\\2t+1=-4\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}t=\dfrac{3}{2}\\t=-\dfrac{5}{2}\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x-2010=\dfrac{3}{2}\\x-2010=-\dfrac{5}{2}\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{4023}{2}\\x=\dfrac{4015}{2}\end{matrix}\right.\)

Trước tiên ta đi chứng minh BĐT phụ là:

Với $a,b>0$ thì $a^2+b^4\ge ab(a^2+b^2)$

Cách CM:

BĐT trên tương đương với: $(a-b{)}^2(a^2+ab+b^2)\ge 0$ (luôn đúng)

Quay trở về bài toán chính: Áp dụng BĐT phụ trên :

$\Rightarrow \frac{c}{a^4+b^4+c}\le \frac{c}{ab(a^2+b^2)+c^{2}ab}=\frac{c}{ab(a^2+b^2+c^2)}=\frac{c^2}{a^2+b^2+c^2}$

Thực hiện tương tự với các phân thức còn lại và cộng theo vế:

$\Rightarrow T\le \frac{a^2+b^2+c^2}{a^2+b^2+c^2}=1$ (đpcm)

Dấu bằng xảy ra khi a=b=c=1

Nó bị mất cái dấu gạch ngang chỗ phân số nha b

a) \(A=\sqrt[]{\left(\sqrt[]{3}-2\right)^2}-\sqrt[]{3}+\sqrt[]{12}\)

\(\Leftrightarrow A=\left|\sqrt[]{3}-2\right|-\sqrt[]{3}+2\sqrt[]{3}\)

\(\Leftrightarrow A=2-\sqrt[]{3}-\sqrt[]{3}+2\sqrt[]{3}\left(2^2=4>\left(\sqrt[]{3}\right)^2=3\right)\)

\(\Leftrightarrow A=2\)

\(B=\left(\dfrac{3\sqrt[]{x}}{\sqrt[]{x}-1}-\dfrac{1}{\sqrt[]{x}+1}-3\right).\dfrac{\sqrt[]{x}+1}{\sqrt[]{x}+2}\left(x\ge0;x\ne1\right)\)

\(\Leftrightarrow B=\left(\dfrac{3\sqrt[]{x}\left(\sqrt[]{x}+1\right)-\left(\sqrt[]{x}-1\right)-3\left(x-1\right)}{\left(\sqrt[]{x}-1\right)\left(\sqrt[]{x}+1\right)}\right).\dfrac{\sqrt[]{x}+1}{\sqrt[]{x}+2}\)

\(\Leftrightarrow B=\left(\dfrac{3x+3\sqrt[]{x}-\sqrt[]{x}+1-3x+3}{\sqrt[]{x}-1}\right).\dfrac{1}{\sqrt[]{x}+2}\)

\(\Leftrightarrow B=\dfrac{2\sqrt[]{x}+4}{\sqrt[]{x}-1}.\dfrac{1}{\sqrt[]{x}+2}\)

\(\Leftrightarrow B=\dfrac{2\left(\sqrt[]{x}+2\right)}{\sqrt[]{x}-1}.\dfrac{1}{\sqrt[]{x}+2}\)

\(\Leftrightarrow B=\dfrac{2}{\sqrt[]{x}-1}\)

b) \(B< -A\)

\(\Leftrightarrow\dfrac{2}{\sqrt[]{x}-1}< -2\) \(\left(x\ge0;x\ne1\right)\)

\(\Leftrightarrow\dfrac{2}{\sqrt[]{x}-1}+2< 0\)

\(\Leftrightarrow\dfrac{2\sqrt[]{x}}{\sqrt[]{x}-1}< 0\)

\(\Leftrightarrow0< \sqrt[]{x}< 1\)

\(\Leftrightarrow0< x< 1\left(thỏa.đkxd\right)\)

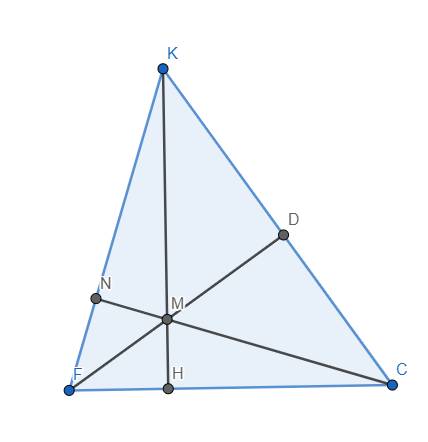
 Dễ thấy \(\widehat{HKF}=\widehat{HCM}\) (cùng phụ với \(\widehat{ABC}\))

 Xét tam giác HKF và HCM, có: \(\widehat{KHF}=\widehat{CHM}\left(=90^o\right)\) và \(\widehat{HKF}=\widehat{HCM}\) (cmt)

 Suy ra \(\Delta HKF~\Delta HCM\left(g.g\right)\)

\(\Rightarrow\dfrac{HK}{HC}=\dfrac{HF}{HM}\) \(\Rightarrow HK.HM=HC.HF\)

 Mà \(HC.HF\le\dfrac{\left(HC+HF\right)^2}{4}=\dfrac{FC^2}{4}\) (BĐT Cô-si), suy ra \(HK.HM\le\dfrac{FC^2}{4}\) (đpcm)

 Dấu "=" xảy ra \(\Leftrightarrow HC=HF\) \(\Leftrightarrow\) H là trung điểm CF \(\Leftrightarrow\Delta KFC\) cân tại K.

Với m = 1 

(d₁) có dạng y = x + 3

(d₂) có dạng y = -x + 3

Phương trình hoành độ giao điểm 

-x + 3 = x + 3

<=> x = 0

Với x = 0 <=> y = 3

Tọa độ giao điểm A(0;3) 

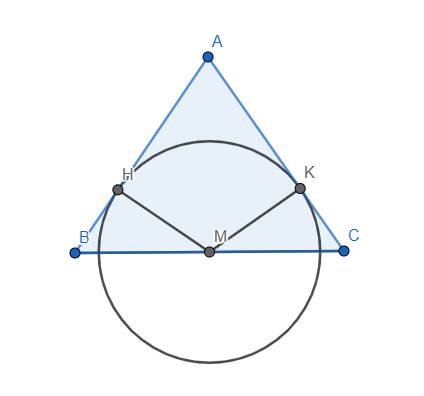
 Gọi K là hình chiếu của M lên AC. Xét tam giác MBH vuông tại H và MCK vuông tại K, ta có:

\(MB=MC\) (M là trung điểm BC); \(\widehat{B}=\widehat{C}\) (tam giác ABC cân tại A)

 \(\Rightarrow\Delta MBH=\Delta MCK\left(ch-gn\right)\)  \(\Rightarrow MH=MK\)

 Ta thấy MK chính là khoảng cách từ AC đến M, đồng thời MK bằng MH là bán kính của đường tròn (M; MH) nên AC tiếp xúc với (M) (đpcm)

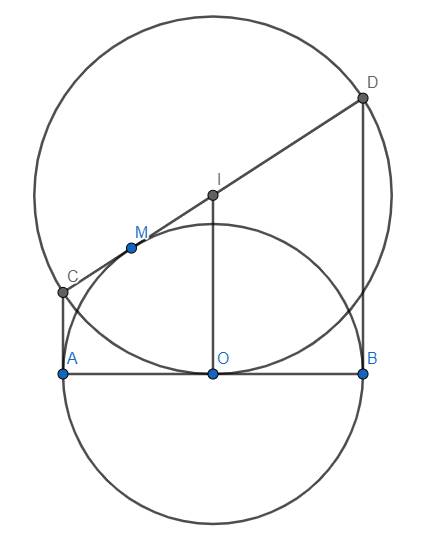
 Dễ thấy ABDC là hình thang. Vì O, I lần lượt là trung điểm của AB, CD nên OI là đường trung bình của hình thang ABDC.

 \(\Rightarrow\left\{{}\begin{matrix}OI//AC//BD\Rightarrow OI\perp AB\left(tạiO\right)\\OI=\dfrac{AC+BD}{2}=\dfrac{CM+DM}{2}=\dfrac{CD}{2}=R\end{matrix}\right.\) với R là bán kính của đường tròn \(\left(CD\right)\).

 Từ đó suy ra AB tiếp xúc (I) tại O. (đpcm)