Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét (O) có
CM,CA là tiếp tuyến
=>CM=CA và OC là phân giác của góc MOA(1)
Xét (O) có
DM,DB là tiếp tuyến
=>DM=DB và OD là phân giác của góc MOB(2)
Từ (1), (2) suy ra góc COD=1/2*góc AOB=90 độ
=>O nằm trên (I)
Xét hình thang ABDC có
O,I lần lượt là trung điểm của AB,CD
=>OI là đường trung bình
=>OI//AC//BD
=>OI vuông góc AB
=>AB tiếp xúc (I) tại O

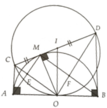
a, Dễ thấy A M B ^ = 90 0 hay E M F ^ = 90 0 tiếp tuyến CM,CA
=> OC ⊥ AM => O E M ^ = 90 0 Tương tự => O F M ^ = 90 0
Chứng minh được ∆CAO = ∆CMO => A O C ^ = M O C ^
=> OC là tia phân giác của A M O ^
Tương tự OD là tia phân giác của B O M ^ suy ra OC ⊥ OD <=> C O D ^
b, Do ∆AOM cân tại O nên OE là đường phân giác đồng thời là đường cao
=> O E M ^ = 90 0 chứng minh tương tự O F M ^ = 90 0
Vậy MEOF là hình chữ nhật
c, Gọi I là trung điểm CD thì I là tâm đường tròn đường kính CD và IO=IC=ID. Có ABDC là hình thang vuông tại A và B nên IO//AC//BD và IO vuông góc với AB. Do đó AB là tiếp tuyến của đường tròn đường kính CD.

a) Tam giác ABC nội tiếp đường tròn (O) đường kính BC
=> OA=OB=OC và O là trung điểm của BC
=> Tam giác ABC vuông tại A
=> góc BAC = 90 độ
b) DO tam giác HAK nội tiếp đường tròn (I)
Lại có góc HAK = 90 độ
=> HK là đường kính của (I)
=> HK đi qua I
=> H,I,K thẳng hàng
c) Đề bài ghi ko rõ
d) 3 điểm nào?
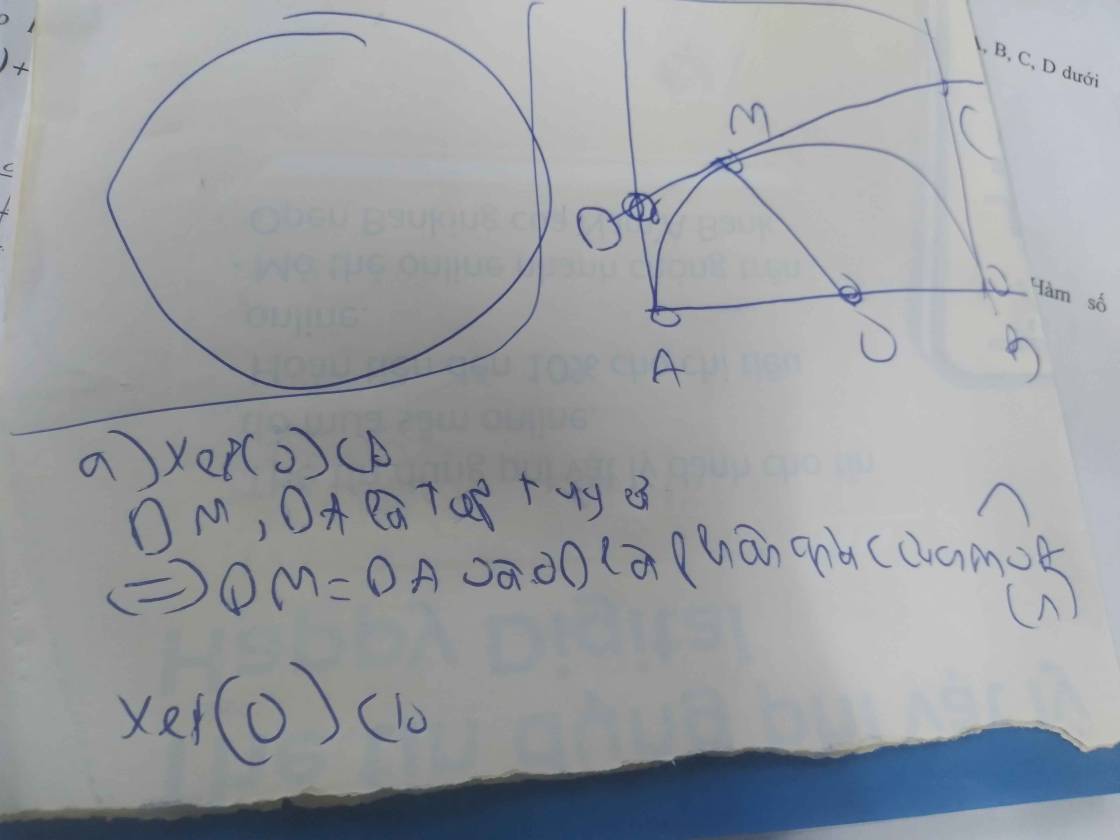

Dễ thấy ABDC là hình thang. Vì O, I lần lượt là trung điểm của AB, CD nên OI là đường trung bình của hình thang ABDC.
\(\Rightarrow\left\{{}\begin{matrix}OI//AC//BD\Rightarrow OI\perp AB\left(tạiO\right)\\OI=\dfrac{AC+BD}{2}=\dfrac{CM+DM}{2}=\dfrac{CD}{2}=R\end{matrix}\right.\) với R là bán kính của đường tròn \(\left(CD\right)\).
Từ đó suy ra AB tiếp xúc (I) tại O. (đpcm)