gtnn |2x - 0.5| + 1/3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


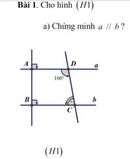
Ta có:a vuông góc với AB
b vuông góc với AB
=>a//b (từ vuông góc đến song song)

`A =|2x-1|+5`
Vì `|2x-1| >= 0`
`-> |2x-1|+5 >= 5`
`->A >= 5`
Dấu "`=`" xảy ra khi : `<=> |2x-1|=0 <=>x=1/2`
Vây `min A=5 <=>x=1/2`

Ta có: |x - 1| \(\ge\)0 với mọi x => |x - 1| + 5 \(\ge\)5
=> A \(\ge\)5
Dấu "=" xảy ra<=> x - 1 = 0 <=> x = 1
Vậy MinA = 5 <=> x= 1
\(A=|x-1|+5\)
Để A nhỏ nhất thì \(|x-1|\)phải nhỏ nhất
Mà: \(|x-1|\ge0\)
\(\Rightarrow\)\(|x-1|\)nhỏ nhất bằng 0
\(\Rightarrow\)\(|x-1|=0\)
\(\Rightarrow\)\(x-1=0\)
\(\Rightarrow\)\(x=1\)
Vậy giá trị nhỏ nhất của A là 5 khi \(x=1\)


1/x-y/6=1/3
ĐKXĐ x khác 0
Ta có
1/x - y/6 = 1/3
<=> 6 - xy = 2x ( nhân cả 2 vế với 6x khác 0 )
<=> 2x + xy = 6
<=> x(2 + y) = 6
Do x, y ∈ Z => x và 2 + y ∈ Z
=> x|6 và 2+y | 6
=> (x , 2+y) = ( -1 ; -6) , (-6 ; -1), ( -2 ; - 3), ( - 3 ; - 2); (1 , 6) , ( 6, 1), (2 , 3) , (3,2)
=> (x,y) = (-1;-8), (-6;-3), (-2;-5), (-3;-4), (1;4), (6;-1), (2;1),(3; 0) ( TM ĐKXĐ)

a) \(5,4+\left(-23,2\right)+4,6+\left(-0,8\right)\)
\(=\left(5,4+4,6\right)+\left(-23,2-0,8\right)=10-24=-14\)
b) \(\left(-14,3\right)+5,1+4,9+\left(-15,7\right)\)
\(=\left(5,1+4,9\right)+\left(-14,3-15,7\right)=10-30=-20\)
c) \(12,3+3,7+\left(-24,2\right)+\left(-12,3\right)+24,2\)
\(=\left(12,3-12,3\right)+\left(-24,2+24,2\right)+3,7=3,7\)
d) \(\left(-16,5\right).3,4+3,4+\left(-3,5\right)\)
\(=3,4\left(-16,5-3,5\right)=3,4\left(-20\right)=-68\)


Vì | 2x - 0,5 | ≥ 0 ∀ x ∈ Z
\(\Rightarrow\left|2x-0,5\right|+\frac{1}{3}\ge\frac{1}{3}\)
Để \(\left|2x-0,5\right|+\frac{1}{3}\)nhận giá trị nhỏ nhất khi \(\left|2x-0,5\right|+\frac{1}{3}=\frac{1}{3}\)
<=> | 2x - 0,5 | = 0
<=> 2x - 0,5 = 0
<=> 2x = 0,5
<=> x = 0,25
`|2x-0,5| + 1/3`
Vì `|2x-0,5| >= 0`
`-> |2x-0,5| +1/3 >= 1/3`
Dấu "=" xảy ra khi : `<=> |2x-0,5|=0 <=> x=1/4`
Vậy GTNN của BT là `1/3 <=> x=1/4`