 giúp mình bài này với
giúp mình bài này với
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


P(\(x\)) = - 5\(x^5\).(- 2\(x^3\))
P(\(x\)) = 10.\(x^8\)
Bậc của đa thức là: 8
Giá trị của đa thức tại \(x\) = -1 là:
P(-1) = 10.(-1)8
P(-1) = 10

Câu 69:
a: Xét ΔBAD vuông tại A và ΔBED vuông tại E có
BD chung
\(\widehat{ABD}=\widehat{EBD}\)
Do đó: ΔBAD=ΔBED
b: Ta có: ΔBAD=ΔBED
=>BA=BE
Ta có: BA+AK=BK
BE+EC=BC
mà BA=BE và AK=EC
nên BK=BC
=>ΔBKC cân tại B
=>\(\widehat{BKC}=\widehat{BCK}\)
c: Xét ΔDAK vuông tại A và ΔDEC vuông tại E có
DA=DE(ΔBAD=ΔBED)
AK=EC
Do đó: ΔDAK=ΔDEC
=>\(\widehat{ADK}=\widehat{EDC}\)
mà \(\widehat{EDC}+\widehat{ADE}=180^0\)(hai góc kề bù)
nên \(\widehat{ADE}+\widehat{ADK}=180^0\)
=>E,K,D thẳng hàng
Ta có: BA=BE
=>B nằm trên đường trung trực của AE(1)
Ta có: DA=DE
=>D nằm trên đường trung trực của AE(2)
Từ (1) và (2) suy ra BD là đường trung trực của AE
=>I nằm trên đường trung trực của AE
=>IA=IE
d: ta có: AD=DE
mà DE<DC(ΔDEC vuông tại E)
nên AD<DC
Câu 70:
a: Ta có; ΔBMC cân tại B
mà BK là đường phân giác
nên BK\(\perp\)MC
Xét ΔBMC có
BK,CA là các đường cao
BK cắt CA tại I
Do đó: I là trực tâm của ΔBMC
=>MI\(\perp\)BC tại H
Xét ΔBAI vuông tại A và ΔBHI vuông tại H có
BI chung
\(\widehat{ABI}=\widehat{HBI}\)
Do đó: ΔBAI=ΔBHI
=>IA=IH và BA=BH
Ta có: BA=BH
=>B nằm trên đường trung trực của AH(1)
ta có: IA=IH
=>I nằm trên đường trung trực của AH(2)
Từ (1) và (2) suy ra BI là đường trung trực của AH
=>BI\(\perp\)AH
mà BI\(\perp\)MC
nên AH//MC
b:
TA có: ΔBMC cân tại B
mà BK là đường phân giác
nên K là trung điểm của MC
ta có: ΔMAC vuông tại A
mà AK là đường trung tuyến
nên AK=MC/2
Ta có: ΔMHC vuông tại H
mà HK là đường trung tuyến
nên HK=MC/2
\(AK+HK=\dfrac{MC}{2}+\dfrac{MC}{2}=MC\)

Câu 3:
x tỉ lệ thuận với y theo hệ số tỉ lệ là 1/3
nên \(x=\dfrac{1}{3}y\)
=>y=3x
=>Không có câu nào đúng
Câu 4:
\(k=x\cdot y=\dfrac{3}{5}\cdot\dfrac{5}{6}=\dfrac{3}{6}=\dfrac{1}{2}\)
=>Không có câu nào đúng
Câu 5: B


Bài 4
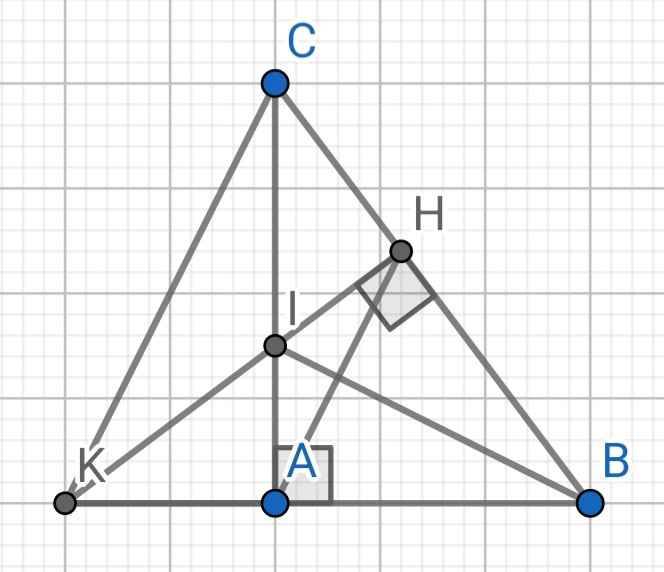
a) Do AB < AC < BC (6 < 8 < 10)
⇒ ∠ACB < ∠ABC < ∠BAC
b) Do BI là tia phân giác của ∠ABC (gt)
⇒ ∠ABI = ∠CBI
⇒ ∠ABI = ∠HBI
Xét hai tam giác vuông: ∆ABI và ∆HBI có:
BI là cạnh chung
∠ABI = ∠HBI (cmt)
⇒ ∆ABI = ∆HBI (cạnh huyền - góc nhọn)
c) Do ∆ABI = ∆HBI (cmt)
⇒ AB = BH (hai cạnh tương ứng)
⇒ B nằm trên đường trung trực của AH (1)
Do ∆ABI = ∆HBI (cmt)
⇒ AI = HI (hai cạnh tương ứng)
⇒ I nằm trên đường trung trực của AH (2)
Từ (1) và (2) ⇒ BI là đường trung trực của AH
d) ∆CHI vuông tại H
⇒ IC là cạnh huyền nên CI là cạnh lớn nhất
⇒ HI < IC
Mà HI = IA (cmt)
⇒ IA < IC
e) ∆ABC vuông tại A (gt)
⇒ CA ⊥ AB
⇒ CA ⊥ BK
⇒ CA là đường cao của ∆BCK
Do IH ⊥ BC (gt)
⇒ KH ⊥ BC
⇒ KH là đường cao của ∆BCK
∆BCK có:
CA là đường cao (cmt)
KH là đường cao (cmt)
Mà I là giao điểm của CA và KH
⇒ BI là đường cao thứ ba của ∆BCK
⇒ BI KC
f) Xét hai tam giác vuông: ∆AIK và ∆HIC có:
AI = HI (cmt)
∠AIK = ∠HIC (đối đỉnh)
⇒ ∆AIK = ∆HIC (cạnh góc vuông - góc nhọn kề)
⇒ IK = IC (hai cạnh tương ứng)
Bài 3:
a: Xét ΔBAK và ΔBIK có
BA=BI
\(\widehat{ABK}=\widehat{IBK}\)
BK chung
Do đó: ΔBAK=ΔBIK
b: Ta có: ΔBAK=ΔBIK
=>\(\widehat{BAK}=\widehat{BIK}\)
=>\(\widehat{BIK}=90^0\)
=>KI\(\perp\)BC
Ta có: ΔBAK=ΔBIK
=>KA=KI
mà KI<KC(ΔKIC vuông tại I)
nên KA<KC
c: Ta có: \(\widehat{CAI}+\widehat{BAI}=\widehat{BAC}=90^0\)
\(\widehat{HAI}+\widehat{BIA}=90^0\)(ΔHAI vuông tại H)
mà \(\widehat{BAI}=\widehat{BIA}\)(ΔBAI cân tại B)
nên \(\widehat{CAI}=\widehat{HAI}\)
=>AI là phân giác của góc HAC
d: Ta có: BA=BI
=>B nằm trên đường trung trực của AI(1)
Ta có: KA=KI
=>K nằm trên đường trung trực của AI(2)
Từ (1) và (2) suy ra BK là đường trung trực của AI
=>BK\(\perp\)AI
Xét ΔBAI có
BK,AH là các đường cao
BK cắt AH tại O
Do đó: O là trực tâm của ΔBAI
=>IO\(\perp\)BA
mà IM\(\perp\)AB
và IM,IO có điểm chung là I
nên I,M,O thẳng hàng
Bài 5:
a: Xét ΔABM và ΔACM có
AB=AC
BM=CM
AM chung
Do đó: ΔABM=ΔACM
b: Ta có: ΔABM=ΔACM
=>\(\widehat{MAB}=\widehat{MAC}\)
Xét ΔAEM vuông tại E và ΔAFM vuông tại F có
AM chung
\(\widehat{EAM}=\widehat{FAM}\)
Do đó: ΔAEM=ΔAFM
=>AE=AF
c: Ta có: AE=AF
=>A nằm trên đường trung trực của EF(1)
Ta có: KE=KF
=>K nằm trên đường trung trực của FE(2)
Ta có: ME=MF(ΔAEM=ΔAFM)
=>M nằm trên đường trung trực của FE(3)
Từ (1),(2),(3) suy ra A,K,M thẳng hàng
d:
Ta có: ΔAMB=ΔAMC
=>\(\widehat{AMB}=\widehat{AMC}\)
mà \(\widehat{AMB}+\widehat{AMC}=180^0\)(hai góc kề bù)
nên \(\widehat{AMB}=\widehat{AMC}=\dfrac{180^0}{2}=90^0\)
=>AM\(\perp\)BC
Ta có: AM\(\perp\) BC
AM//DC
Do đó: DC\(\perp\)BC
Ta có: \(\widehat{ACD}+\widehat{ACB}=\widehat{DCB}=90^0\)
\(\widehat{ADC}+\widehat{ABC}=90^0\)(ΔDCB vuông tại C)
mà \(\widehat{ACB}=\widehat{ABC}\)(ΔABC cân tại A)
nên \(\widehat{ACD}=\widehat{ADC}\)
=>AC=AD
mà AB=AC
nên AB=AD
=>A là trung điểm của BD


Tỉ số phần trăm chính là tỉ số của hai số mà ở đây, ta sẽ phải thực hiện quy đồng mẫu số của những tỉ số đó về 100. Ký hiệu: %. Ví dụ: 50% tương đương với 50/100, hoặc là 0.5. Đọc là năm mươi phần trăm.






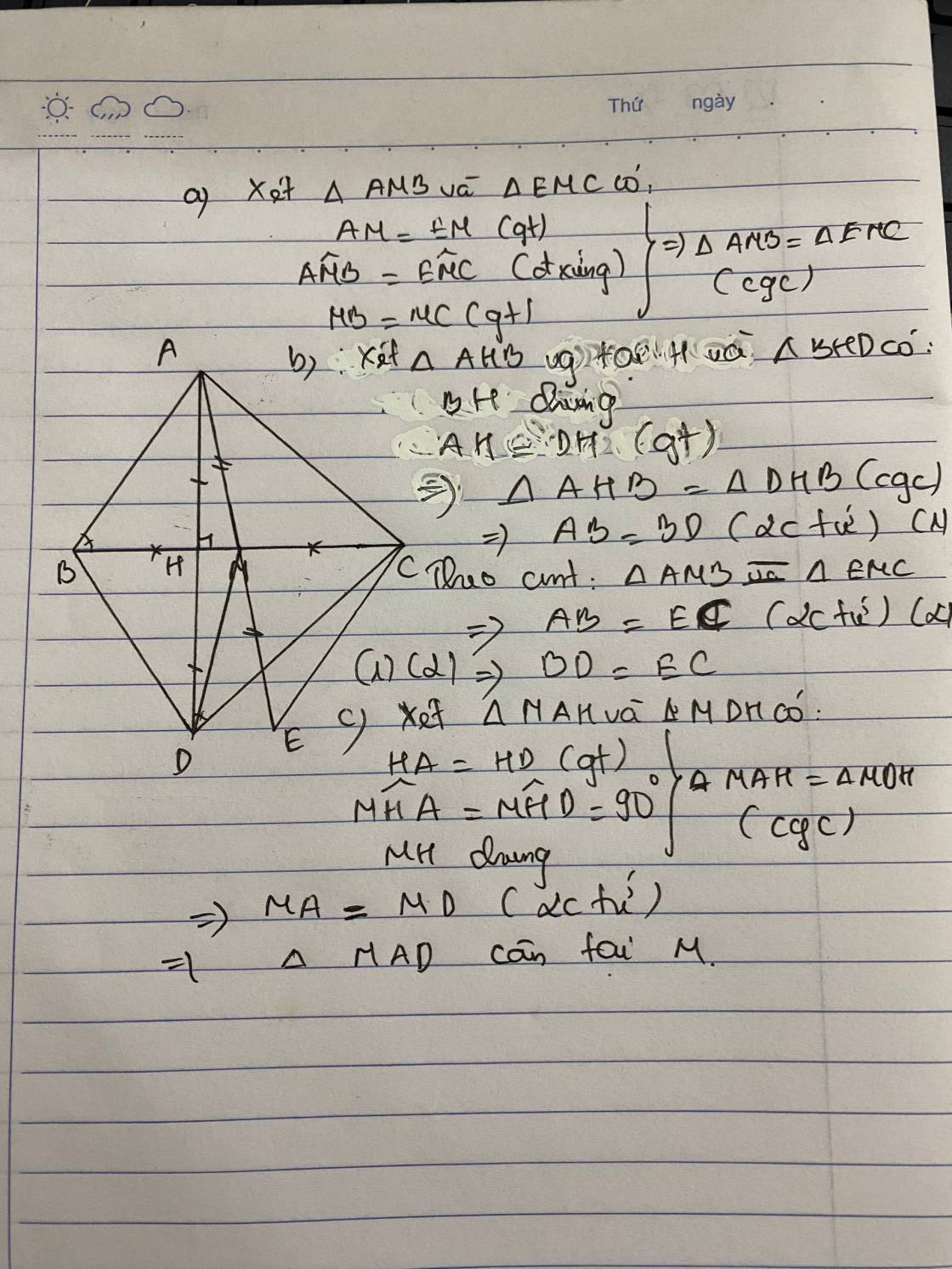
a: Xét ΔNMB và ΔNEB có
NM=NE
\(\widehat{MNB}=\widehat{ENB}\)
NB chung
Do đó: ΔNMB=ΔNEB
b: Ta có; ΔNMB=ΔNEB
=>\(\widehat{NMB}=\widehat{NEB}\)
=>\(\widehat{NEB}=90^0\)
=>BE\(\perp\)NC
c: Ta có;ΔNMB=ΔNEB
=>BM=BE
mà BE<BC(ΔBEC vuông tại E)
nên BM<BC
d: Xét ΔBMH vuông tại M và ΔBEC vuông tại E có
BM=BE
MH=EC
Do đó: ΔBMH=ΔBEC
=>\(\widehat{MBH}=\widehat{EBC}\)
mà \(\widehat{EBC}+\widehat{MBE}=180^0\)(hai góc kề bù)
nên \(\widehat{MBH}+\widehat{MBE}=180^0\)
=>E,B,H thẳng hàng