Nếu f(1)=2 thì:

\(2+a+b+6=2\)

\(\Rightarrow a+b=-6\)

Nếu f(-1)=12 thì:

\(-2+a-b+6=12\)

\(\Rightarrow a-b=8\)

Giá trị a và b thoả mãn là rất lớn nên mình không lập bảng.

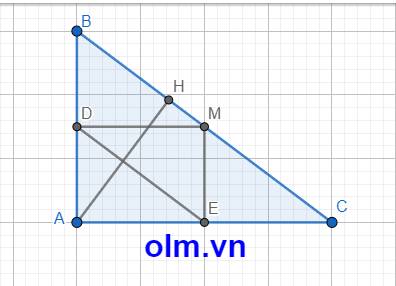
 a, Xét tứ giác DMEC có: \(\widehat{D}\) = \(\widehat{A}\) = \(\widehat{C}\) = 90⁰

⇒ Tứ giác DMEC là hình chữ nhật 

⇒ AM = DE 

b, MD \(\perp\) AB; AB \(\perp\) AC ⇒ MD// AC 

Xét tam giác: ABC có:

MD//AC; MB = MC ⇒ AD = DB ^{(vì trong tam giác đường thằng đi qua trung điểm một cạnh và song song với cạnh thứ hai thì nó đi qua điểm của cạnh còn lại)} 

Chứng minh tương tự ta có: EA = EC

Xét tam giác ABC có: AD = DB 

                                   MB = MC

 ⇒ DM song song và bằng CE

  ⇒ DMCE là hình bình hành

c, Chứng minh tương tự ý b ta có 

       DE // BC

Xét tam giác vuông ABH vuông tại H; DB = DA ⇒ HD = DB = AD

ME = AD = DB (vì ADME là hình chữ nhật)

⇒ HD = ME 

⇒ DMHE là hình thang cân.

d, DE//BC ⇒ DE \(\perp\) AH; DA = DH ⇒ DE là trung trực của AH ⇒

A đối xứng với H qua DE 

a) Đơn thức là \(2,5xy^3;x^4;-0,7x^3y^2;x^3.x^2;-\dfrac{3}{4}x^2ỹ^3;-3,6\)

b) \(5x^2.3xy^2=15x^3y^2\)

\(\dfrac{1}{5}xy^2z.\left(-5xy\right)=-x^2y^3z\)

\(\dfrac{1}{4}\left(x^2y^3\right).\left(-2xy\right)=-\dfrac{1}{2}x^3y^4\)

c) \(\left(-7x^2yz\right).\dfrac{3}{7}xy^2z^3=-3x^3y^3z^4\rightarrow bậc10\)

\(-\dfrac{2}{3}xy^2z.\left(-3x^2y\right)^2=-\dfrac{2}{3}xy^2z.9x^4y^2=-6x^5y^4z\rightarrow bậc10\)

\(\left(-2x^2y\right).\left(-\dfrac{1}{2}\right)^2.\left(x^2y^3\right)^2=\left(-2x^2y\right).\dfrac{1}{4}.x^4y^6=-\dfrac{1}{2}x^6y^7\rightarrow bậc13\)

a/

FB=FC (gt); FD=FG (gt) => BDCG là hình bình hành (Tứ giác có hai đường chéo cắt nhau tại trung điểm mỗi đường là hbh)

b/

Ax//BC => AH//FB

Fy//AB => FH//AB

=> ABFH là hbh (Tứ giác có các cặp cạnh đối // với nhau từng đôi một là hbh)

=> AH=FB (cạnh đối hbh); Mà FB=FC => AH=FC

Ta có Ax//BC => AH//FC

=> AFCH là hbh (Tứ giác có 1 cặp cạnh đối // và = nhau là hbh)

=> AF//HC (cạnh đối hbh)

c/

DA=DB (gt)

FB=FC (gt)

=> J là trọng tâm của tg ABC \(\Rightarrow AJ=\dfrac{2}{3}AF\)

\(HK=\dfrac{1}{3}HC\Rightarrow CK=\dfrac{2}{3}HC\)

Ta có AFCH là hbh (cmt) =>AF=HC

=> AJ=CK (Tứ giác có 1 cặp cạnh đối // và = nhau là hbh)

Ta có

AF//HC (cmt) => AJ//CK

=>AKCJ là hbh 

Nối J với K cắt AC tại I'

=> I'A=I'C (trông hbh hai đường chéo cắt nhau tại trung điểm mỗi đường) => I' là trung điểm AC

Mà I cũng là trung điểm AC

\(\Rightarrow I'\equiv I\) => J; I; K thẳng hàng

Ta có:

2n² + n - 7 = n² - 4n + 5n - 10 + 3

= (2n² - 4n) + (5n - 10) + 3

= 2n(n - 2) + 5(n - 2) + 3

Để (2n² + n - 7)/(n - 2) là số nguyên thì 3 ⋮ (n - 2)

⇒ n - 2 ∈ Ư(3) = {-3; -1; 1; 3}

⇒ n ∈ {-1; 1; 3; 5}

a) \(x^2+xy+y^2+1\)

\(=x^2+xy+\dfrac{y^2}{4}-\dfrac{y^2}{4}+y^2+1\)

\(=\left(x+\dfrac{y}{2}\right)^2+\dfrac{3y^2}{4}+1\)

mà \(\left\{{}\begin{matrix}\left(x+\dfrac{y}{2}\right)^2\ge0,\forall x;y\\\dfrac{3y^2}{4}\ge0,\forall x;y\end{matrix}\right.\)

\(\Rightarrow\left(x+\dfrac{y}{2}\right)^2+\dfrac{3y^2}{4}+1>0,\forall x;y\)

\(\Rightarrow dpcm\)

b) \(...=x^2-2x+1+4\left(y^2+2y+1\right)+z^2-6z+9+1\)

\(=\left(x-1\right)^2+4\left(y^{ }+1\right)^2+\left(z-3\right)^2+1>0,\forall x.y\)

\(\Rightarrow dpcm\)