Bài tập tự luận: sự đồng quy của ba đường trung tuyến SVIP

Hướng dẫn giải:

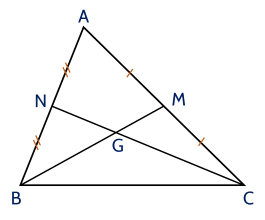
Xét tam giác $ABC$ có hai đường trung tuyến $BM$ và $CN$ cắt nhau tại $G$.

Suy ra $G$ là trọng tâm tam giác $ABC$

$\Rightarrow BG=\dfrac{2}{3} BM$; $CG=\dfrac{2}{3} CN$

$ \Rightarrow BM=\dfrac{3}{2} BG$; $CN=\dfrac{3}{2} CG$.

Do đó ta phải chứng minh $\dfrac{3}{2} B G+\dfrac{3}{2} C G>\dfrac{3}{2} B C$ hay $B G+C G>B C$. (1)

Bất đẳng thức (1) luôn đúng vì trong một tam giác tổng độ dài hai cạnh lớn hơn độ dài cạnh còn lại.

Vậy $BM+CN>\dfrac{3}{2} BC$. (điều phải chứng minh).

Hướng dẫn giải:

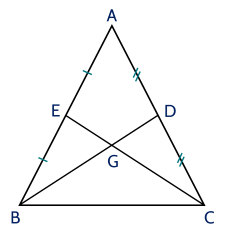
a) Ta có $\triangle ABC$ cân tại $A \Rightarrow AB=AC$ mà $AB=2 BE$; $AC=2 CD$ (vì $E, \, D$ theo thứ tự là trung điểm của $AB$, $AC)$.

Do đó ta có $2 BE=2 CD$ hay $BE=CD$.

Xét $\triangle BCE$ và $\triangle CBD$ có $BE=CD$ (chứng minh trên);

$\widehat{EBC}=\widehat{DCB}$;

$BC$ là cạnh chung.

Do đó $\triangle BCE=\triangle CBD$ (c.g.c)

$\Rightarrow CE=BD$ (hai cạnh tương ứng).

b) Ta có $G$ là trọng tâm tam giác $ABC$ nên $B G=\dfrac{2}{3} BD$ và $CG=\dfrac{2}{3} CE$ (tính chất trọng tâm).

Mà $CE=BD$ (phần a) nên $\dfrac{2}{3} CE=\dfrac{2}{3} BD$ hay $CG=BG$.

Vậy tam giác $GBC$ cân tại $G$.

c) Ta có $GB=\dfrac{2}{3} BD \Rightarrow GD=\dfrac{1}{3} BD \Rightarrow GB=2 GD \Rightarrow GD=\dfrac{1}{2} GB$

Chứng minh tương tự, ta có $GE=\dfrac{1}{2} GC$.

Do đó $GD+GE=\dfrac{1}{2} GB+\dfrac{1}{2} GC=\dfrac{1}{2}(GB+GC)$.

Mà $GB+GC>BC$ (trong một tam giác tổng độ dài hai cạnh lớn hơn cạnh còn lại).

Do đó $GD+GE>\dfrac{1}{2} BC$ (điều phải chứng minh).

Hướng dẫn giải:

a) Xét tam giác $ABD$ có $C$ là trung điểm của cạnh $AD \Rightarrow BC$ là trung tuyến của tam giác $ABD$.

Hơn nữa $G \in BC$ và $GB=2 GC \Rightarrow GB=\dfrac{2}{3} BC \Rightarrow G$ là trọng tâm tam giác $ABD$.

Lại có $AE$ là đường trung tuyến của tam giác $ABD$ nên $A, \, G, \, E$ thẳng hàng.

b) Ta có $G$ là trọng tâm tam giác $ABD \Rightarrow DG$ là đường trung tuyến của tam giác này.

Suy ra $DG$ đi qua trung điểm của cạnh $AB$ (điều phài chứng minh).

Hướng dẫn giải:

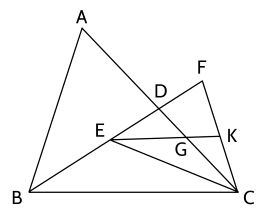
a) Ta có $BF=2 BE \Rightarrow BE=EF$.

Mà $BE=2 ED$ nên $EF=2 ED \Rightarrow D$ là trung điểm của $EF \Rightarrow CD$ là đường trung tuyến của tam giác $EFC$.

Vì $K$ là trung điểm của $CF$ nên $EK$ là đường trung tuyến của $\triangle EFC$.

$\triangle EFC$ có hai đường trung tuyến $CD$ và $EK$ cắt nhau tại $G$ nên $G$ là trọng tâm của $\triangle EFC$.

b) Ta có $G$ là trọng tâm tam giác $EFC$ nên $\dfrac{GC}{DC}=\dfrac{2}{3}$ và $G E=\dfrac{2}{3} E K$

$\Rightarrow GK=\dfrac{1}{3} EK \Rightarrow GE=2 GK \Rightarrow \dfrac{GE}{GK}=2$.

Hướng dẫn giải:

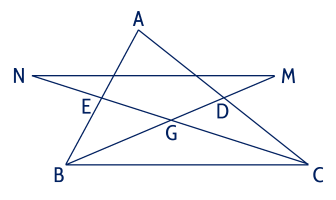
a) Ta có $DM=DG \Rightarrow GM=2 GD$.

Ta lại có $G$ là giao điểm của $BD$ và $CE \Rightarrow G$ là trọng tâm của tam giác $ABC$

$ \Rightarrow BG=2 GD$.

Suy ra $BG=GM$.

Chứng minh tương tự ta được $CG=GN$.

b) Xét tam giác $GMN$ và tam giác $GBC$ có $GM=GB$ (chứng minh trên);

$\widehat{MGN}=\widehat{BGC}$ (hai góc đối đỉnh);

$GN=GC$ (chứng minh trên).

Do đó $\triangle GMN=\triangle GBC$ (c.g.c)

$\Rightarrow MN=BC$ (hai cạnh tương ứng).

Theo chứng minh trên $\triangle GMN=\triangle GBC \Rightarrow \widehat{NMG}=\widehat{CBG}$ (hai góc tương ứng).

Mà $\widehat{NMG}$ và $\widehat{CBG}$ ờ vị trí so le trong nên $MN$ // $BC$.

Hướng dẫn giải:

Gọi $D$ là giao điểm của $AG$ và $BC \Rightarrow DB=DC$.

Ta có $B G=\dfrac{2}{3} B E$; $C G=\dfrac{2}{3} C F$ (tính chất trọng tâm).

Vì $BE=CF$ nên $BG=CG \Rightarrow \triangle B C G$ cân tại $G$

$ \Rightarrow \widehat{G C B}=\widehat{G B C}$

Xét $\triangle B F C$ và $\triangle C E B$ có $C F=B E$ (giả thiết);

$\widehat{G C B}=\widehat{G B C}$ (chứng minh trên);

$B C$ là cạnh chung.

Do đó $\triangle B F C=\triangle C E B$ (c.g.c)

$\Rightarrow \widehat{F B C}=\widehat{E C B}$ (hai góc tưong ứng)

$\Rightarrow \triangle A B C$ cân tại $A \Rightarrow A B=A C$.

Từ đó suy ra $\triangle A B D=\triangle A C D$ (c.c.c)

$\Rightarrow \widehat{A D B}=\widehat{A D C}$. (hai góc tương ứng)

Mà $\widehat{A D B}+\widehat{A D C}=180^{\circ} \Rightarrow \widehat{A D B}=\widehat{A D C}=90^{\circ} \Rightarrow A D \perp B C$ hay $A G \perp B C$.