3 mũ mấy vậy bạn . Bạn đánh lại đề nha.

3^n nha

Bài 1:

a) Diện tích xung quanh: 

\(S_{xq}=\left(5+4\right)\cdot2\cdot3=54\left(dm^2\right)\)

Diện tích toàn phần:

\(S_{tp}=54+5\cdot4\cdot2=94\left(dm^2\right)\)

b) Diện tích xung quanh là:

\(S_{xq}=\left(\dfrac{3}{5}+\dfrac{10}{3}\right)\cdot2\cdot\dfrac{2}{3}\approx5,24\left(m^2\right)\)

Diện tích toàn phần:

\(S_{tp}=5,24+\dfrac{3}{5}\cdot\dfrac{10}{3}\cdot2=9,24\left(m^2\right)\)

Bài 2 :

a) Diện tích xung quanh bể bơi :

\(\left(4+3,5\right).2.1,5=22,5\left(m^2\right)\)

Diện tích đá cần dùng để lát bể bơi :

\(22,5+4.3,5=36,5\left(m^2\right)\)

b) Số tiền cần dùng để mua đá lát bể bơi :

\(36,5.250000=9125000\left(đồng\right)\)

Đáp số...

cảm ơn cô ạ

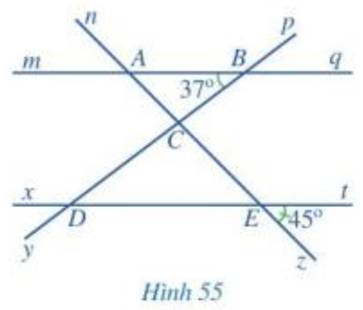
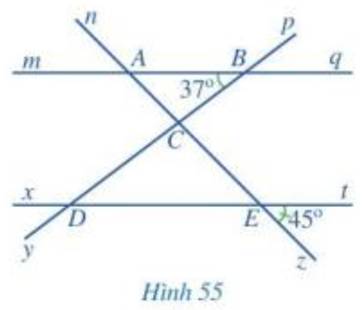
a, Các góc đồng vị bằng nhau là:

\(\widehat{nAm}\) = \(\widehat{AEx}\);    \(\widehat{mAE}\) = \(\widehat{zED}\);  \(\widehat{nAB}\) = \(\widehat{AEt}\)

 \(\widehat{qAE}\) = \(\widehat{tEz}\);   \(\widehat{pBq}\) = \(\widehat{BDE}\);  \(\widehat{qBC}\) = \(\widehat{EDy}\); \(\widehat{pBA}\) = \(\widehat{BDx}\); \(\widehat{ABD}\)=\(\widehat{xDy}\)

b, Các góc so le trong:

 \(\widehat{ABC}\) = \(\widehat{CDE}\);    \(\widehat{mAC}\) = \(\widehat{CEt}\);    \(\widehat{BAC}\) = \(\widehat{CED}\); \(\widehat{qBc}\) = \(\widehat{CDx}\)

c, \(\widehat{BAC}\) = \(\widehat{zEt}\) = 45⁰

    \(\widehat{CDE}\) = \(\widehat{ABC}\) = 39⁰ 

d, \(\widehat{BCE}\) = \(\widehat{CDE}\) + \(\widehat{CED}\) (góc ngoài tam giác bằng tổng hai góc trong không kề với nó.

  \(\widehat{CED}\) = \(\widehat{zEt}\) = 45⁰ (hai góc đối đỉnh)

\(\widehat{BCE}\) = 39⁰ + 45⁰ = 84⁰

Bài 1:

a) \(3^7:3^5-\left(\dfrac{5}{17}\right)^0=3^{7-5}-1=3^2-1=9-1=8\)

b) \(\left(\dfrac{5}{2}\right)^{13}:\left(\dfrac{1}{2}+2\right)^3\)

\(=\left(\dfrac{5}{2}\right)^{13}:\left(\dfrac{5}{2}\right)^3\)

\(=\left(\dfrac{5}{2}\right)^{10}\)

c) \(8.\left(\dfrac{1}{4}\right)^3+\left(\dfrac{2}{27}\right)^0-\dfrac{1}{8}\)

\(=8.\dfrac{1}{64}+1-\dfrac{1}{8}\)

\(=\dfrac{1}{8}+1-\dfrac{1}{8}\)

\(=1\)

Bài 2:

a) \(\dfrac{3^4.4^4}{6^4}=\dfrac{3^4.\left(2^2\right)^4}{\left(2.3\right)^4}=\dfrac{3^4.2^8}{2^4.3^4}=\dfrac{2^8}{2^4}=2^4=16\)

b) \(\dfrac{15^3}{10^3}=\dfrac{\left(3.5\right)^3}{ \left(2.5\right)^3}=\dfrac{3^3.5^3}{2^3.5^3}=3^3:2^3=\dfrac{27}{8}\)

c) \(\dfrac{4^2.12^5}{9^2.2^{10}}=\dfrac{\left(2^2\right)^2.\left[3.\left(2^2\right)\right]^5}{\left(3^2\right)^2.2^{10}}=\dfrac{2^4.3^5.2^{10}}{3^4.2^{10}}=2^4.3=16.3=48\)

d) \(\dfrac{6^2+5.2^2+4}{15}=\dfrac{\left(2.3\right)^2+5.2^2+2^2}{15}=\dfrac{2^2.3^2+5.2^2+2^2}{15}=\dfrac{2^2\left(3^2+5+1\right)}{15}=\dfrac{2^2.15}{15}=2^2=4\)

Bài 3:

a) \(\dfrac{\left(\dfrac{2}{3}\right)^3.\left(\dfrac{-3}{4}\right)^2.\left(-1\right)^5}{\left(\dfrac{2}{5}\right)^2.\left(\dfrac{-5}{12}\right)^2}\)

\(=\dfrac{\left(\dfrac{2}{3}\right)^3.\left(\dfrac{-3}{4}\right)^2.-1}{\left[\dfrac{2}{5}.\left(\dfrac{-5}{12}\right)\right]^2}\)

\(=\dfrac{\left(\dfrac{2}{3}\right)^3. \left(\dfrac{-3}{4}\right)^2.-1}{\left(\dfrac{-1}{6}\right)^2}\)

\(=\left(\dfrac{2}{3}\right)^3.\left[\left(\dfrac{-3}{4}\right).-6\right]^2.-1\)

\(=\left(\dfrac{2}{3}\right)^3.\left(\dfrac{9}{2}\right)^2.-1\)

\(=\left(\dfrac{2}{3}\right)^2.\dfrac{2}{3}.\left(\dfrac{9}{2}\right)^2.-1\)

\(=\left(\dfrac{2}{3}.\dfrac{9}{2}\right)^2.\dfrac{2}{3}.-1\)

\(=9.\dfrac{2}{3}.-1\)

\(=6.-1=-6\)

b) \(\dfrac{6^6+6^3.3^3+3^6}{-73}=\dfrac{\left(2.3\right)^6+\left(2.3\right)^3.3^3+3^6}{-73}=\dfrac{2^6.3^6+2^3.3^3.3^3+3^6}{-73}=\dfrac{2^6.3^6+2^3.3^6+3^6}{-73}=\dfrac{3^6\left(2^6+2^3+1\right)}{-73}=\dfrac{3^6.73}{-73}=\dfrac{3^6}{-1}=\left(-3\right)^6\)

\(#Wendy.Dang\)

Lần sau bnn gửi từng bài thôi nha, chứ như vầy nhiều quá thì làm không nổi mất. đánh máy nãy giờ lú luôn gòi nè :))

a) \(5^6:5^5+\left(\dfrac{4}{9}\right)^0=5^{6-5}+1=5+1=6\)

b) \(\left(\dfrac{3}{7}\right)^{21}:\left(1-\dfrac{40}{49}\right)^3\)

\(=\left(\dfrac{3}{7}\right)^{21}:\left(\dfrac{9}{49}\right)^3\)

\(=\left(\dfrac{3}{7}\right)^{21}:\left[\left(\dfrac{3}{7}\right)^2\right]^3\)

\(=\left(\dfrac{3}{7}\right)^{21}:\left(\dfrac{3}{7}\right)^6\)

\(=\left(\dfrac{3}{7}\right)^{21-6}=\left(\dfrac{3}{7}\right)^{15}\)

c) \(\left(\dfrac{2}{3}\right)^3-\left(\dfrac{-52}{3}\right)^0+\dfrac{4}{9}\)

\(=\dfrac{8}{27}-1+\dfrac{4}{9}\)

\(=\dfrac{8-27+12}{27}=-\dfrac{7}{27}\)

\(a)5^6:5^5+\left(\dfrac{4}{9}\right)^0=5^1+1=6\)

\(b,\left(\dfrac{3}{7}\right)^{21}:\left(1-\dfrac{40}{49}\right)^3\)

\(=\left(\dfrac{3}{7}\right)^{21}:\left(\dfrac{49-40}{49}\right)^3\)

\(=\left(\dfrac{3}{7}\right)^{21}:\left(\dfrac{9}{49}\right)^3=\left(\dfrac{3}{7}\right)^{21}:[\left(\dfrac{3}{7}\right)^2]^3\)

\(=\left(\dfrac{3}{7}\right)^{21}:\left(\dfrac{3}{7}\right)^6=\left(\dfrac{3}{7}\right)^{21-6}\)

\(=\left(\dfrac{3}{7}\right)^{15}\)

\(c,3.\left(\dfrac{2}{3}\right)^3-\left(\dfrac{-52}{3}\right)^0+\dfrac{4}{9}\)

\(=3.\dfrac{8}{27}-1+\dfrac{4}{9}\)

\(=\dfrac{8}{9}-1+\dfrac{4}{9}\)

\(=\dfrac{8-9+4}{9}=\dfrac{1}{3}\)

Thể tích bể bơi là: 12 x 10 x 1,2 = 144 (m³)

Gọi lượng nước mà mỗi máy bơm cần bơm vào bể lần lượt là:

\(x;y;z\) (m³);  \(x;y;z>0\)

Theo bài ra ta có:  \(\dfrac{x}{7}=\dfrac{y}{8}=\dfrac{z}{9}\)

Áp dụng tính chất dãy tỉ số bằng nhau ta có:

    \(\dfrac{x}{7}=\dfrac{y}{8}=\dfrac{z}{9}\) = \(\dfrac{x+y+z}{7+8+9}\) = \(\dfrac{144}{24}\) = 6

\(x\) = 6 x 7 = 42

y = 6 x 8 = 48

z = 6 x 9 = 54 

Kết luận lượng nước mà mỗi máy cần bơm để hồ đầy theo thứ tự lần lượt là:

      42 m³; 48 m³; 54 m³

Thể tích bể:

12 . 10 . 1,2 = 144 (m³)

Gọi x (m³), y (m³), z (m³) lần lượt là số m³ mà máy bơm thứ nhất, máy bơm thứ hai và máy bơm thứ ba phải bơm (x, y, z > 0)

Ta có: x + y + z = 144 (m³)

Do lượng nước bơm được của ba máy tỉ lệ với 7; 8; 9 nên:

x/7 = y/8 = z/9

Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:

x/7 = y/8 = z/9 = (x + y + z)/(7 + 8 + 9) = 144/24 = 6

x/7 = 6 ⇒ x = 7.6 = 42 (nhận)

y/8 = 6 ⇒ y = 8.6 = 48 (nhận)

z/9 = 6 ⇒ z = 9.6 = 54 (nhận)

Vậy số m³ nước ba máy bơm để đầy bể lần lượt là: 42 m³, 48 m³, 54 m³