

Đào Đức Vinh
Giới thiệu về bản thân



































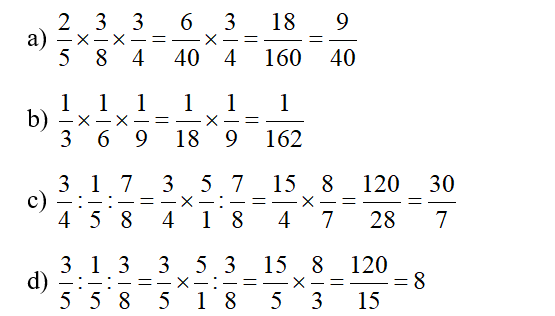
6.25
Ta có: a3 + b3 + ab = (a + b)3 – 3ab(a + b) + ab
= 1 – 3ab + ab (do a + b = 1)
= 1 – 2ab = 1 – 2a( 1 – a)
= 2a2 – 2a + 1 =
.
Vậy (đpcm).
Lời giải
Theo đề, ta có x + y + z + 2 = xyz
⇔ (xy + yz + zx) + 2(x + y + z) + 3 = xyz + xy + yz + zx + x + y + z + 1
⇔ (x + 1)(y + 1) + (y + 1)(z + 1) + (z + 1)(x + 1) = (xy + x + y + 1)(z + 1)
⇔ (x + 1)(y + 1) + (y + 1)(z + 1) + (z + 1)(x + 1) = (x + 1)(y + 1)(z + 1)
.
Đặt
Khi đó ta có a + b + c = 1 và .
Ta có .
(hiển nhiên theo bất đẳng thức Bunhiacopski)
Dấu “=” xảy ra .
Vậy ta có điều phải chứng minh.
Nguyên tử khối của X là: MX = 3,5.16 = 56
X là Fe
62376525.5363
Nồng độ mol (ký hiệu: CM) là một đại lượng dùng để biểu thị nồng độ của một chất tan trong dung dịch. Nó cho biết số mol chất tan có trong 1 lít dung dịch. Tính thể tích dung dịch (V): Đổi đơn vị thể tích về lít. Áp dụng công thức: Thay các giá trị đã tính được vào công thức CM = n/V để tính nồng độ mol.\
có hơn 70 ngôi đền ở chăm-ba
vãi vật lí lớp 5 á mày hack à
Nếu không có lực cản của không khí thì hạt mưa có thể được coi như một vật rơi tự do.
Vận tốc chạm đất: