
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


ĐKXĐ: \(x\in\left[0;2018\right]\)
\(y'=\dfrac{1009-x}{\sqrt{2018x-x^2}}=0\Rightarrow x=1009\)
Hàm đồng biến trên \(\left(0;1009\right)\)

Gọi tọa độ các giao điểm là \(A\left(a;0;0\right)\); \(B\left(0;b;0\right)\); \(C\left(0;0;c\right)\)
Không làm mất tính tổng quát, chỉ cần xét trường hợp \(a;b;c>0\)
Phương trình mặt phẳng (P) theo đoạn chắn: \(\frac{x}{a}+\frac{y}{b}+\frac{z}{c}=1\)
Ta có: \(S=OA+OB+OC=a+b+c\)
Do \(\left(P\right)\) qua M nên: \(\frac{4}{a}+\frac{1}{b}+\frac{9}{c}=1\)
Áp dụng BĐT Cauchy-Scwarz: \(\frac{2^2}{a}+\frac{1^2}{b}+\frac{3^2}{c}\ge\frac{\left(2+1+3\right)^2}{a+b+c}=\frac{36}{a+b+c}\)
\(\Rightarrow\frac{36}{a+b+c}\le1\Rightarrow a+b+c\ge36\)
\(\Rightarrow S_{min}=36\) khi \(\left\{{}\begin{matrix}a+b+c=36\\\frac{2}{a}=\frac{1}{b}=\frac{3}{c}\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=12\\b=6\\c=18\end{matrix}\right.\)
Phương trình (P) khi đó có dạng: \(\frac{x}{12}+\frac{y}{6}+\frac{z}{18}=1\)
Hay chuyển dạng chính tắc: \(3x+6y+2z-36=0\)
Không thấy điểm I ở đâu để tính tiếp cả, nhưng đến đây thì mọi chuyện đơn giản, chỉ cần áp dụng công thức khoảng cách vào là xong.

Chọn C
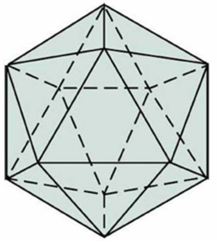
Khối hai mươi mặt đều có các mặt là tam giác nên thuộc loại 3 ; 5 .

Gọi A là điểm biểu diễn số phức z
Khi đó A nằm trên đường trung trực của đoạn thẳng đi qua hai điểm (0;2) và (2;4). Ta tìm được pt đường thẳng đó là: d: x+y-4=0
|z|=OA min khi và chỉ khi A là hình chiếu của O trên d
Khi đó ta tìm được A(2;2)
->min|z|=\(2\sqrt{2}\)


\(\left\{{}\begin{matrix}\overrightarrow{AB}=\left(-1;y+3;-5\right)\\\overrightarrow{AC}=\left(x-2;7;-1\right)\end{matrix}\right.\)
\(A;B;C\) thẳng hàng \(\Rightarrow\frac{-1}{x-2}=\frac{y+3}{7}=\frac{-5}{-1}\)
\(\Rightarrow\left\{{}\begin{matrix}x-2=-\frac{1}{5}\\y+3=35\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=\frac{9}{5}\\y=32\end{matrix}\right.\) \(\Rightarrow10x+y=50\)

a) f' (x)=3x2-6x
f'' (x)=6x-6;f'' (x)=0 < ⇒ x=1 ⇒ f (1) = -1
Vậy I(1; -1)
b) Công thức chuyển hệ trục tọa độ trong phép tịnh tiến theo vectơ OI:
Phương trình của (C) đối với hệ trục IXY là:
y - 1 = (X+1)3-3(X+1)2+1 hay Y=X3-3X
Vì hàm số Y=X3-3X là hàm số lẻ nên đồ thị của nó nhận gốc tọa độ I làm tâm đối xứng.
c) * Tiếp tuyến với (C) tại I(1; -1) đối với hệ tọa độ Oxy là:
y = f' (1)(x-1)+f(1) với f’(1) = -3; f(1) = -1
Nên Phương trình tiếp tuyến: y= -3(x-1)+(-1) hay y = -3x + 2
Xét hiệu (x3-3x2+1)-(-3x+2)=(x-1)3
Với x ∈(-∞;1) ⇒ (x-1)3<0 ⇔ x3 – 3x2 + 1 < -3x +2 nên đường cong (C): y=x3-33+1 nằm phía dưới tiếp tuyến y = -3x + 2
Với x ∈(1; +∞) ⇒ (x-1)3>0 ⇔ x3 – 3x2 + 1 > -3x + 2 nên đường cong (C): nằm phía trên tiếp tuyến tại I.






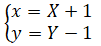
Olm xin kính chào bạn, hiện tại câu hỏi của bạn chưa hiển thị đấy có thể là do file mà bạn tải lên bị lỗi nên đã không hiển thị trên diễn đàn. Bạn nên viết đề bài trực tiếp trên Olm. Như vậy bạn sẽ không mắc phải lỗi file đề như vậy. Điều này giúp bạn nhanh chóng nhận được sự trợ giúp từ cộng đồng olm. Cảm ơn bạn đã đồng hành cùng Olm nhé!