Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: \(18\cdot7+65:13\)
=126+5
=131
b: \(785-\dfrac{323+148}{3}+2781\)
\(=785+2781-\dfrac{471}{3}\)
=3566-157
=3409
c: \(703-\dfrac{140}{42+28}-17^6\cdot17^9:17^{13}\)
\(=703-\dfrac{140}{70}-17^2\)
\(=703-289-2\)
=703-291
=412
e: \(\left(2^3\cdot9^4+9^3\cdot45\right):\left(9^2\cdot10-9^2\right)\)
\(=\dfrac{9^3\left(2^3\cdot9+45\right)}{9^2\cdot\left(10-1\right)}=\dfrac{9^3}{9^3}\cdot\left(8\cdot9+45\right)\)
=72+45
=117


Ta có:
\(\frac{A}{B}=\frac{\frac{2000}{1}+\frac{1999}{2}+\frac{1998}{3}+...+\frac{1}{2000}+2000}{1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+...+\frac{1}{2000}}\)
\(\Leftrightarrow\frac{A}{B}=\frac{\left(\frac{2000}{1}+1\right)+\left(\frac{1999}{2}+1\right)+\left(\frac{1998}{3}+1\right)+...+\left(\frac{1}{2000}+1\right)+2000+1}{1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+...+\frac{1}{2000}}\)
\(\Leftrightarrow\frac{A}{B}=\frac{\frac{2001}{1}+\frac{2001}{2}+\frac{2001}{3}+...+\frac{2001}{2000}+2001}{1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+...+\frac{1}{2000}}\)
\(\Leftrightarrow\frac{A}{B}=\frac{2001\left(1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+...+\frac{1}{2000}\right)}{1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+...+\frac{1}{2000}}\)
\(\Leftrightarrow\frac{A}{B}=2001\)
bn cộng trên tử rồi thì phải trừ đi chứ ko phân số sẽ thay đổi

\(B=2+2^2+2^3+2^4+...+2^{99}+2^{100}=2\left(1+2^2+2^3+2^4\right)+...+2^{96}\left(1+2^2+2^3+2^4\right)=2.31+2^6.31+...+2^{96}.31=31\left(2+2^6+...+2^{96}\right)⋮31\)


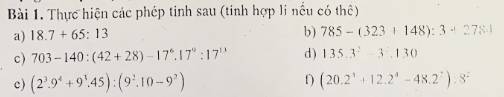 giúp mình với ạ mai mih nộp bài ruii🥶
giúp mình với ạ mai mih nộp bài ruii🥶
2000
\(2000x1999-1999^2+1^{2024}\\ =2000x1999-1999x1999+1\\ =1999\left(2000-1999\right)+1\\ =1999x1+1\\ =1999+1\\ =2000\)