tm x,biết;\(\frac{x+1}{10}+\frac{x+1}{11}+\frac{x+1}{12}=\frac{x+1}{13}+\frac{x+1}{14}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




a.
\(\Leftrightarrow x\left(y+1\right)^2=32y\Leftrightarrow x=\dfrac{32y}{\left(y+1\right)^2}\)
Do y và y+1 nguyên tố cùng nhau \(\Rightarrow32⋮\left(y+1\right)^2\)
\(\Rightarrow\left(y+1\right)^2=\left\{4;16\right\}\)
\(\Rightarrow...\)
b.
\(2a^2+a=3b^2+b\Leftrightarrow2\left(a-b\right)\left(a+b\right)+a-b=b^2\)
\(\Leftrightarrow\left(2a+2b+1\right)\left(a-b\right)=b^2\)
Gọi \(d=ƯC\left(2a+2b+1;a-b\right)\)
\(\Rightarrow b^2\) chia hết \(d^2\Rightarrow b⋮d\) (1)
Lại có:
\(\left(2a+2b+1\right)-2\left(a-b\right)⋮d\)
\(\Rightarrow4b+1⋮d\) (2)
(1);(2) \(\Rightarrow1⋮d\Rightarrow d=1\)
\(\Rightarrow2a+2b+1\) và \(a-b\) nguyên tố cùng nhau
Mà tích của chúng là 1 SCP nên cả 2 số đều phải là SCP (đpcm)

Đặt \(\left(x;y;z\right)=\left(a;b;c\right)\) (em ko có ý gì cả, chỉ là gõ quen tay hơn thôi:V)
Đặt \(p=a+b+c;q=ab+bc+ca;r=abc\)
Quy vể: Tìm min, max của P = p biết p, q, r > 0 thỏa mãn \(p^2-2q-p\le\frac{4}{3}\)
Ta có: \(\frac{4}{3}\ge p^2-2q-p\ge\frac{1}{3}p^2-p\)
Do đó \(\frac{1}{3}p^2-p-\frac{4}{3}\le0\Leftrightarrow-1\le p\le4\)
Do đó....
P/s: đúng ko ạ?

x+x+1+x+2 = 99
x.3 +1+2 = 99
x .3 +1 = 99 - 2
x.3 +1 = 97
x.3 = 97 - 1
x.3 = 96
x = 96 : 3
x = 32

Giải:
\(\left|x+1\right|+\left|x+2\right|+\left|x+3\right|+\left|x+4\right|=5x\)
\(\ge\left|x+1+x+2+x+3+x+4\right|=5x\)
\("="\Leftrightarrow\left|4x+10\right|=5x\)
\(\Leftrightarrow\left[{}\begin{matrix}4x+10=5x\\4x+10=-5x\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=10\left(n\right)\\x=-\dfrac{10}{9}\left(l\right)\end{matrix}\right.\)
Vậy ...
Ta có
\(\left|x+1\right|\ge0\)
\(\left|x+2\right|\ge0\)
\(\left|x+3\right|\ge0\)
\(\left|x+4\right|\ge0\)
=> \(\left|x+1\right|+\left|x+2\right|+\left|x+3\right|+\left|x+4\right|\ge0\)
=> 5x\(\ge0\)
Dấu "=" xảy ra <=>
x+1+x+2+x+3+x+4=5x
=> (x+x+x+x)+(1+2+3+4)=5x
=> 4x+10=5x
=> 5x-4x=10
=> x=10
Vậy x=10
cô giáo mk dạy vậy đó , nên chắc chắn là đúng


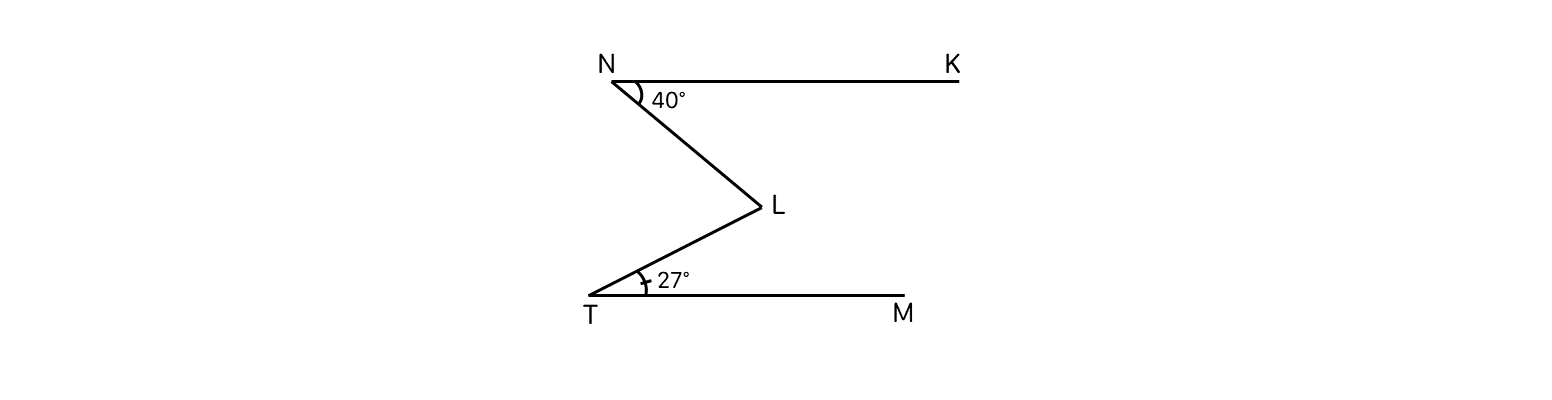
\(\widehat{NLT}=360^0-140^0-153^0=220^0-153^0=67^0\)
\(\Leftrightarrow\left(x+1\right)\left(\frac{1}{10}+\frac{1}{11}+\frac{1}{12}-\frac{1}{13}-\frac{1}{14}\right)=0\)
Vì \(\left(\frac{1}{10}+\frac{1}{11}+\frac{1}{12}-\frac{1}{13}-\frac{1}{14}\right)>0\)=> x = -1.
Vế sau đâu bạn?