a: PTHĐGĐ là:

x^2-3x+2=0

=>(x-2)(x-1)=0

=>x=2 hoặc x=1

Khi x=2 thì y=2^2=4

Khi x=1 thì y=1^2=1

b: Δ=(2m+2)^2-4(2m-3)

=4m^2+8m+4-8m+12

=4m^2+16>0

=>Phương trình luôn có hai nghiệm

Vì (d1)//(d) nên \(\left\{{}\begin{matrix}a=3\\b\ne-4\end{matrix}\right.\)

Vậy: (d1): y=3x+b

Thay x=-2 vào (P), ta được:

\(y=\dfrac{1}{2}\cdot\left(-2\right)^2=\dfrac{1}{2}\cdot4=2\)

Thay x=-2 và y=2 vào (d1), ta được:

\(3\cdot\left(-2\right)+b=2\)

\(\Leftrightarrow b=8\)(thỏa ĐK)

Vậy: (d1): y=3x+8

để \(\left(d1\right)\) sogn song với \(\left(d\right)\)

\(< =>\left\{{}\begin{matrix}a=3\\b\ne-4\end{matrix}\right.\)

để (d1) cắt (P) tại A có hoành độ -2\(=>x=-2\)

\(=>\dfrac{1}{2}x^2=3x+b< =>\dfrac{1}{2}\left(-2\right)^2=3\left(-2\right)+b=>b=8\left(tm\right)\) 

=>\(\left(d1\right):y=3x+8\)

1: f(2)=2^2=4

=>A thuộc (P)

2: bạn bổ sung lại đề đi bạn

Đủ mà

Phương pháp:

Diện tích hình phẳng (H) giới hạn bởi đồ thị hàm số 

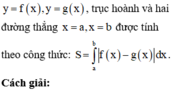
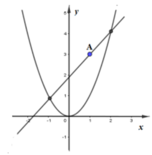
Diện tích hình phẳng giới hạn bởi parabol (P) và đường thẳng d:

S = ∫ x 1 x 2 k x − k + 3 − x 2 d x = 1 2 k x 2 − k − 3 x − 1 3 x 3 x 2 x 1 = 1 2 k x 1 2 − k − 3 x 1 − 1 3 x 1 3 − 1 2 k x 2 2 − k − 3 x 2 − 1 3 x 2 3 = 1 2 k x 1 2 − x 2 2 − k − 3 x 1 − x 2 − 1 3 x 1 3 − x 2 3 = x 1 − x 2 1 2 k x 1 + x 2 − k − 3 − 1 3 x 1 + x 2 2 − x 1 x 2 = x 1 − x 2 1 2 k . k − k − 3 − 1 3 k 2 − k − 3 = x 1 − x 2 1 6 k 2 − 2 3 k + 2

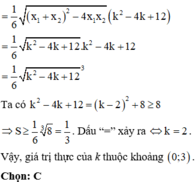
Đường thẳng d và parabol (P) tiếp xúc với nhau khi phương trình a. x 2 = m.x + n ↔a. x 2 − m.x – n = 0 vô nghiệm (∆< 0)

Đáp án: C

1: PTHĐGĐ là:

x^2-x-m+1=0(1)

Δ=(-1)^2-4(-m+1)=1+4m-4=4m-3

Để (P) cắt (d) tại hai điểm phân biệt thì 4m-3>0

=>m>3/4

Để (1) có hai nghiệm dương phân biệt thì m>3/4 và 1>0 và -m+1>0

=>m>3/4 và -m>-1

=>3/4<m<1