Chọn D.

Gọi d: y=ax+ b

Đường thẳng d đi qua N( 1; -1) nên -1= a+ b

Và   suy ra b= -2.

Vậy hàm số cần tìm là  y= x-2.

Chọn B.

Đáp án D

Chọn D

Đáp án D

Đáp án C

sao a phải nhỏ hơn 0

a: Thay x=4 và y=1 vào y=(m+1)x-3, ta được:

4(m+1)-3=1

=>4m+4-3=1

=>4m+1=1

hay m=0

b: Để hai đường vuông góc thì 5(m+1)=-1

=>m+1=-1/5

hay m=-6/5

c: Thay x=2 vào y=3x-1, ta được:

\(y=3\cdot2-1=5\)

Thay x=2 và y=5 vào (d), ta được:

2(m+1)-3=5

=>2(m+1)=8

=>m+1=4

hay m=3

Đáp án D

Gọi hàm số cần tìm là y= ax + b

Đường thẳng d cắt trục Ox tại 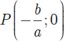 và cắt Oy tại Q( 0 ;b) với a< 0; b> 0

Ta có tam giác OPQ cân tại O nên 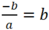 hay b( a+1) =0

Suy ra b=0 (loại) hoặc a= -1

Ta có d qua M nên 2=a+ b nên b= 3

Vậy hàm số cần tìm là y= -x+ 3. 

Chọn D.

a: Thay x=2 và y=-3 vào (d), ta được:

\(2\left(2m-1\right)-2m+5=-3\)

=>\(4m-2-2m+5=-3\)

=>2m+3=-3

=>2m=-6

=>\(m=-\dfrac{6}{2}=-3\)

b: Để (d)//(d') thì \(\left\{{}\begin{matrix}2m-1=2\\-2m+5\ne1\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}2m=3\\-2m\ne-4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m=\dfrac{3}{2}\\m\ne2\end{matrix}\right.\)

=>m=3/2

Thay m=3/2 vào (d), ta được:

\(y=\left(2\cdot\dfrac{3}{2}-1\right)x-2\cdot\dfrac{3}{2}+5=2x+2\)

y=2x+2 nên a=2

Gọi \(\alpha\) là góc tạo bởi (d) với trục Ox

\(tan\alpha=2\)

=>\(\alpha\simeq63^026'\)

a: Để hàm số là hàm số bậc nhất thì 2m-3<>0

hay m<>3/2

b: Để hàm số đồng biến thì 2m-3>0

hay m>3/2

Để hàm số nghịch biến thì 2m-3<0

hay m<3/2