Giả sử hàm số y=f(x) liên tục, nhận giá trị dương trên 0 ; + ∞ và thỏa mãn f(1)=1, f ( x ) = f ' ( x ) 3 x + 1 , với mọi x>0. Mệnh đề nào sau đây đúng?
![]()
![]()
![]()
![]()
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Ta có f x = f ' x 3 x + 1
⇔ f ' x f x = 1 3 x + 1 ⇔ ∫ f ' x f x d x = ∫ d x 3 x + 1
⇔ ∫ a f x f x = ∫ 3 x + 1 − 1 2 d x
⇔ ln f x = 2 3 3 x + 1 + C ⇔ f x = e 2 3 3 x + 1 + C
Mặt khác f 1 = 1
suy ra 1 = e 4 3 + C
⇔ C = − 4 3 ⇒ f 5 ≈ 3 , 793

Chọn C.
Phương pháp : Đưa biểu thức đã cho về dạng y ' y = g x và lấy nguyên hàm hai vế.
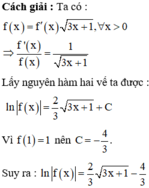
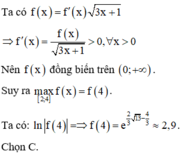
Chọn D