cho đoạn thẳng AB . Trong cùng 1 nửa mặt phẳng AB , ta kẻ 2 tia Ax, By cùng vuông góc với đường thẳng AB ; 1 điểm C trên tia Ax và 1 điểm D thuộc tia By sao cho hệ thức sau đây được thỏa mãn: AB2 = 4AC.BD
a) C/m hệ thức CD2=IC2+ID2
b) C/m các tam giác AIC,BDI và IDC đồng dạng với nhau
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1:Gọi giao của DO và CB là H
Xét ΔOAD vuông tại A và ΔOBH vuông tại B có
OA=OB
góc AOD=góc BOH
=>ΔOAD=ΔOBH
=>OD=OH
=>ΔCDH cân tại C
=>ΔAOD đồng dạng với ΔBOH
Xét ΔBOH vuông tại B và ΔOCH vuông tại O có
góc BHO chung
=>ΔBOH đồng dang với ΔOCH
=>ΔAOD đồng dạng với ΔOCH
2: ΔCHD cân tại C
=>góc CDH=góc CHD=góc ADH
=>DH là phân giác của góc ADC

*Độc giả tự vẽ hình, người giải ko biết cách đăng hình:))*
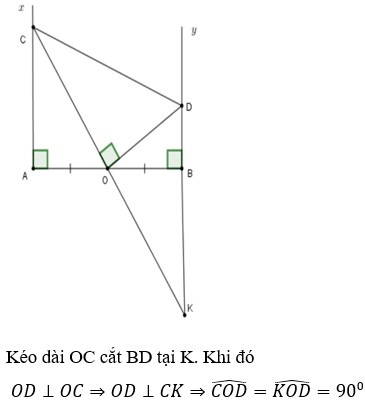
Gọi giao điểm của CO và BD là Z
Xét 2 tam giác vuông AOC và BOZ có:
OA=OB (O là trung điểm AB)
Góc AOC = góc BOZ (đối đỉnh)
Suy ra: tam giác AOC = tam giác BOZ (cgv-gn)
Do đó: AC=BZ và OC=OZ (các cặp cạnh tương ứng)
Vì OC=OZ nên O là trung điểm CZ => OD là đường trung tuyến tam giác DCZ (1)
Vì OD vuông góc OC nên OD là đường cao tam giác DCZ (2)
Từ (1) và (2) suy ra: tam giác DCZ cân tại D (có OD vừa là đường cao vừa là đường trung tuyến) => CD=DZ (3)
Mặt khác: DZ=BD+BZ
Mà: AC=BZ (cmt)
Nên: DZ=BD+AC (4)
Từ (3) và (4) suy ra: CD=BD+AC (đpcm)





a: AB^2=4*AC*BD
=>4*AI*BI=4*AC*BD
=>AI*BI=AC*BD
=>AI/BD=AC/BI
=>ΔAIC đồng dạng với ΔBDI
=>góc AIC=góc BDI
=>góc AIC+góc BID=90 độ
=>góc CID=90 độ
=>CD^2=IC^2+ID^2
b: ΔAIC đồng dạng với ΔBDI(cmt)
Gọi M là giao của CI với BD
Xét ΔIAC vuông tại A và ΔIBM vuông tại B có
IA=IB
góc AIC=góc BIM
=>ΔIAC=ΔIBM
=>AC=BM và IC=IM
=>góc ICD=góc IMD
=>góc ICD=góc ACI
=>ΔICD đồng dạng với ΔACI
=>ĐPCM