Ba số x, y, z theo thứ tự lập thành một cấp số nhân với công bội q khác 1 ; đồng thời các số x ; 2y ; 3z theo thứ tự lập thành một cấp số cộng với công sai khác 0. Tìm giá trị của q.
A. q = 1 3 .
B. q = 1 9 .
B. q = − 1 3 .
D. q = − 3.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
16 tháng 9 2018
Chọn B
Giả sử ba số hạng a, b, c lập thành cấp số cộng thỏa yêu cầu, khi đó b, a, c theo thứ tự đó lập thành cấp số nhân công bội q. Ta có
a + c = 2 b a = b q ; c = b q 2 ⇒ b q + b q 2 = 2 b ⇔ b = 0 q 2 + q − 2 = 0 .
Nếu b = 0 ⇒ a = b = c = 0 nên a, b, c là cấp số cộng công sai d= 0 (vô lí).
Nếu q 2 + q − 2 = 0 ⇔ q = 1 hoặc q= -2. Nếu q = 1 ⇒ a = b = c (vô lí), do đó q = -2.
CM
13 tháng 12 2018
Gọi công bội của CSN x ; y ; z là q.
⇒ y = x.q ; z = x.q2.
Lại có : x ; 2y ; 3z lập thành CSC
⇔ 2y – x = 3z – 2y
⇔ 2.xq – x = 3.xq2 – 2.xq
⇔ x(2q – 1) = x.(3q2 – 2q)
⇔ x.(3q2 – 4q + 1) = 0
+ Nếu x = 0 ⇒ y = z = 0
⇒ q không xác định.
+ Nếu x ≠ 0 ⇒ 3q2 – 4q + 1 = 0 ⇔ q = 1 hoặc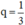 
Vậy CSN có công bội q = 1 hoặc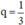 
CM
9 tháng 1 2018
Đáp án B
Vì x , y , z > 0 theo thứ tự lập thành 1 CSN nên z = q y = q 2 x .
Vì log a x , log a y , log a 3 z theo thứ tự lập thành cấp số cộng nên 2 log a y = log a x + log a 3 z
⇔ 4 log a y = log a x + 3 log a z ⇔ 4 log a q x = log a x + 3 log a q 2 x ⇔ log a q 4 x 4 = log a x q 3 x 3
⇔ q 4 x 4 = q 6 x 4 ⇒ q = 1 ⇒ x = y = z ⇒ P = 1959 + 2019 + 60 = 4038
Chọn A
Theo giả thiết ta có :
y = x q ; z = x q 2 x + 3 z = 2 2 y ⇒ x + 3 x q 2 = 4 x q ⇒ x 3 q 2 − 4 q + 1 = 0 ⇔ x = 0 3 q 2 − 4 q + 1 = 0 .
Nếu x = 0 ⇒ y = z = 0 ⇒ công sai của cấp số cộng: x ; 2y ; 3z bằng 0 (vô lí).
nếu
3 q 2 − 4 q + 1 = 0 ⇔ q = 1 q = 1 3 ⇔ q = 1 3 q = 1 .