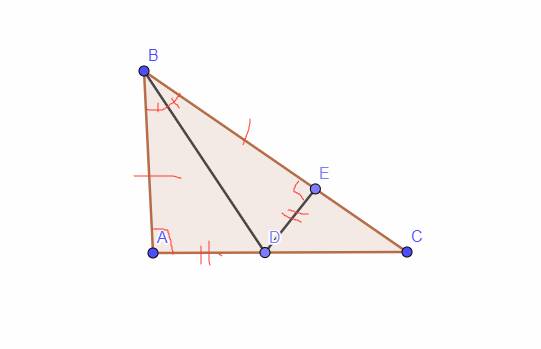
Cho tam giác ABC vuông tại A (AB < AC), tia phân giác của góc B cắt cạnh AC tại D. Vẽ DC vuông góc với BC tại E
a) Chứng minh tam giác ABD = EBD
b) Cho AB=6 cm; AC=8 c. Tính BC và EC
c) I là giao điểm của ED và BA. Chứng minh tam giác BIC cân
d) So sánh AD và DC

.jpg)

a: Xét ΔABD vuông tại A và ΔEBD vuông tại E có
BD chung
\(\widehat{ABD}=\widehat{EBD}\)
Do đó:ΔABD=ΔEBD
b: \(BC=\sqrt{AB^2+AC^2}=10\left(cm\right)\)
c: Xét ΔADI vuông tại A và ΔEDC vuông tại E có
DA=DE
\(\widehat{ADI}=\widehat{EDC}\)
Do đó:ΔADI=ΔEDC
Suy ra: AI=EC
Ta có: BA+AI=BI
BE+EC=BC
mà BA=BE
và AI=EC
nên BI=BC
hayΔBIC cân tại B
d: Ta có: AD=DE
mà DE<DC
nên AD<DC
Cảm ơn bạn nhìu nha