Cho hình vuông ABCD cạnh a, E ∈ BC, F ∈ AD sao cho CE = AF; AE, BF cắt CD lần lượt tại M, N.
a) cm: CM.DN không đổi.
b) K là giao điểm của AN và BM. cm : góc MKN = 90o.
c) Các điểm E, F có vị trí như thế nào để MN bé nhất
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét tứ giác AECF có
AE//CF
AE=CF
Do đó: AECF là hình bình hành
Suy ra: AF//CE
Xét hình tứ giác đấy có:
`=>AE//// CF`
`AE=CF`
Có bốn cạnh như trên suy ra là hình bình hành.
`=>` `AF////CE`

a) Theo hệ quả của định lý Thales ta có:
\(\dfrac{DN}{AB}=\dfrac{AF}{FD};\dfrac{CM}{AB}=\dfrac{CE}{EB}\Rightarrow\dfrac{DN}{AB}.\dfrac{CM}{AB}=\dfrac{AF}{FD}.\dfrac{CE}{EB}=1\Rightarrow DN.CM=a^2\).
b) Do \(CM.DN=a^2=AD.BC\Rightarrow\dfrac{CM}{BC}=\dfrac{AD}{DN}\).
Mà \(\widehat{MCB}=\widehat{ADN}=90^o\Rightarrow\Delta NDA\sim\Delta BCM\left(c.g.c\right)\Rightarrow\widehat{AND}=\widehat{MBC}\Rightarrow\widehat{AND}+\widehat{MCB}=\widehat{MBC}+\widehat{MCB}=90^o\Rightarrow\widehat{MKN}=90^o\).
c) Áp dụng bất đẳng thức AM - GM:
\(DN+CM\ge2\sqrt{DN.CM}=2a\).
Do đó \(MN=DN+DC+CM\ge2a+a=3a\).
Đẳng thức xảy ra khi và chỉ khi DN = CM \(\Leftrightarrow DN=CM=a\)
\(\Leftrightarrow\) E, F lần lượt là trung điểm của BC, DA.

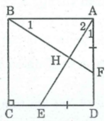
Xét ∆ ABF và ∆ DAE,ta có: AB = DA (gt)
∠ (BAF) = ∠ (ADE) = 90 0
AF = DE (gt)
Suy ra: ΔABF = ΔDAE (c.g.c)
⇒ BF = AE và ∠ B 1 = ∠ A 1
Gọi H là giao điểm của AE và BF.
Ta có: ∠ (BAF) = ∠ A 1 + ∠ A 2 = 90 0
Suy ra: ∠ B 1 + ∠ A 2 = 90 0
Trong ΔABH,ta có: ∠ (AHB) + ∠ B 1 + ∠ A 2 = 180 0
⇒ ( ∠ (AHB) ) = 180 0 – ( ∠ B 1 + ∠ A 2 ) = 180 0 – 90 0 = 90 0
Vậy AE ⊥ BF

Có tam giác BHCBHC ∼AFH∼AFH
Vì AFBC=AEAB=AHBHAFBC=AEAB=AHBH
và gHBC=FAHgHBC=FAH (c−g−c)(c−g−c)
⇒BHC=AHF⇒BHC=AHF mà AHF+BHF=90⇒BHF+BHC=90AHF+BHF=90⇒BHF+BHC=90=> FH VUÔNG GÓC HC
⇒⇒ đpcm.

Bài 3:
a: Xét ΔCDF vuông tại C và ΔBCE vuông tại B có
CD=BC
CF=BE
Do đó: ΔCDF=ΔBCE
=>góc CDF=góc BCE
=>góc BCE+góc MFC=góc DFC+góc CDF=90 độ
=>CE vuông góc với DF
b: Gọi Klà trung điểm của CD và N là giao của AK và DF
Xét tứ giác AECK có
AE//CK
AE=CK
Do dó: AECK là hình bình hành
SUy ra: AK=CE và AK//CE
=>AK vuông góc với DF
Xét ΔDMC có
K là trung điểm của DC
KN//MC
Do đó: N là trung điểm của DM
Xét ΔAMD có
AN vừa là đường cao, vừa là đường trung tuyến
nên ΔAMD cân tại A
Hình vẽ:
Lời giải:
a) $AF=CE, AD=BC\Rightarrow DF=BE$
Vì $ABCD$ là hình vuông nên $AB\parallel CD$
$\Rightarrow AB\parallel DN, CM$. Áp dụng định lý Talet:
\(\frac{AB}{DN}=\frac{AF}{DF}=\frac{CE}{BE}\)
$\frac{AB}{CM}=\frac{BE}{CE}$
Nhân theo vế 2 đẳng thức trên suy ra:
$\frac{AB^2}{DN.CM}=1\Rightarrow DN.CM=AB^2$ không đổi.
b) Do $ABCD$ là hình vuông nên:
$DN.CM=AB^2=AD.BC$
$\Rightarrow \frac{DN}{AD}=\frac{BC}{CM}$
$\Rightarrow \triangle DAN\sim \triangle CMB$ (c.g.c)
$\Rightarrow \widehat{AND}=\widehat{MBC}=90^0-\widehat{BMC}$
hay $\widehat{KNM}=90^0-\widehat{KMN}$
$\Rightarrow \triangle KMN$ vuông tại $K$
$\Rightarrow \widehat{MKN}=90^0$
c)
$MN=DN+CM+DC=DN+CM+AB\geq 2\sqrt{DN.CM}+AB$ theo BĐT AM-GM$
hay $MN\geq 2\sqrt{AB^2}+AB=3AB$
Vậy $MN_{\min}=3AB$. Giá trị này đạt được khi $DN=CM$
$\Leftrightarrow \frac{DN}{AB}=\frac{CM}{AB}$
$\Leftrightarrow \frac{DF}{FA}=\frac{EC}{BE}$
$\Leftrightarrow \frac{BE}{EC}=\frac{EC}{BE}$
$\Leftrightarrow BE=EC$ hay $E$ là trung điểm của $BC$. Điều này kéo theo $F$ là trung điểm của $AD$.