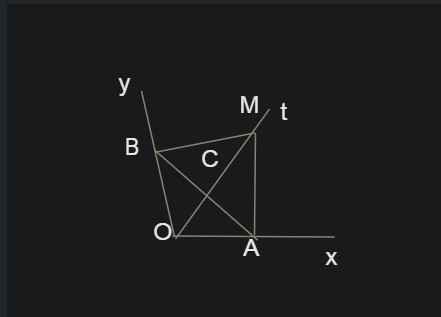
Cho góc nhọn xOy . Trên tia phân giác Ot của góc xOy lấy điểm M . Từ M hạ các đường vuông góc MA \(⊥\)Ox và MB \(⊥\)Oy ( A \(∈\)Ox ; B \(∈\)Oy )
a) Chứng minh rằng tam giác OMA = tam giác OMB
b) Chứng minh rằng 2 tam giác OAB và MAB là 2 tam giác cân

a, Vì Ot là phân giác của xOy
=> xOt = tOy = xOy/2
Xét △OAM vuông tại A và △OBM vuông tại B
Có: AOM = MOB
OM là cạnh chung
=> △OAM = △OBM (cgv-gn)
b, Vì △OAM = △OBM
=> OA = OB (2 cạnh tương ứng)
=> AM = BM (2 cạnh tương ứng)
Xét △OAB có: OA = OB
=> △OAB cân tại O
Xét △ABM có: AM = BM
=> △ABM cân tại M