Cho tam giác ABC cân tại A, đường phân giác góc B cắt AC tại D. Đường phân giác góc C cắt AB tại E . Cho biết AB = 15cm ; BC = 10cm .
a ) Cm : BD = CE .
b ) Cm : DE // BC .
c ) Tính AD, CD, DE .
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vì BE ⊥ BD nên BE là đường phân giác góc ngoài tại đỉnh B
Suy ra : 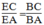 ( t/chất đường phân giác)
( t/chất đường phân giác)
Suy ra: 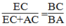 ⇒ EC.BA= BC (EC + AC)
⇒ EC.BA= BC (EC + AC)
Suy ra: EC.BA - EC.BC = BC.AC ⇒EC (BA - BC) = BC.AC
Vậy 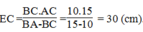

a: Xét ΔABC có BD là phân giác
nên AD/AB=CD/BC
=>AD/15=CD/10
=>AD/3=CD/2=(AD+CD)/(3+2)=15/5=3
=>AD=9cm; CD=6cm
b: BE vuông góc BD
=>BE là phân giác góc ngoài tại B
=>EC/EA=BC/BA
=>EC/(EC+15)=10/15=2/3
=>3EC=2EC+30
=>EC=30cm

Vì BD là đường phân giác của ∠ (ABC) nên:
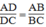 (t/chất đường phân giác)
(t/chất đường phân giác)
Suy ra: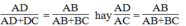
Mà ΔABC cân tại A nên AC = AB = 15 (cm)
Suy ra: AD/15 = 15/(15+10) ⇒ AD = (15.15)/25 = 9(cm)
Vậy DC = AC – AD = 15 – 9 = 6 (cm)


Vì BD là đường phân giác của A B C ^ nên: A D D C = A B B C
Suy ra: A D D C + A D = A B B C + A B (theo tính chất dãy tỉ số bằng nhau)
⇒ A D A C = A B B C + A B
Mà tam giác ABC cân tại A nên AC = AB = 15cm
Đáp án: C


a.Ta có CDCD là phân giác góc C
→DA\DB=CA\CB=2→DA\DA+DB=2\2+1
→DA\AB=2\3
→DA=2\3AB=2\3AC=16(AB=AC)
→BD=AB−AD=8
b.Vì CE⊥CD,CD là phân giác trong của ΔABC
→CElà phân giác ngoài ΔABC
→EB\EA=CB\CA=1\2
→BE\EA−EB=1\2−1
→BE\AB=1
→BE=AB=AC=24
.Ta có CDCD là phân giác góc C
→DADB=CACB=2→DADA+DB=22+1→DADB=CACB=2→DADA+DB=22+1
→DAAB=23→DAAB=23
→DA=23AB=23AC=16(AB=AC)→DA=23AB=23AC=16(AB=AC)
→BD=AB−AD=8→BD=AB−AD=8
b.Vì CE⊥CD,CDCE⊥CD,CD là phân giác trong của ΔABCΔABC
→CE→CE là phân giác ngoài ΔABCΔABC
→EBEA=CBCA=12→EBEA=CBCA=12
→BEEA−EB=12−1→BEEA−EB=12−1
→BEAB=1→BEAB=1
→BE=AB=AC=24
![]() ....
....

a) ta có
goc BAD+ goc DAC =90 (2 góc kề phụ)
goc ADB+goc HAD=90 ( tam giác AHD vuông tại H)
goc DAC=goc HAD (AD lả p/g goc HAC)
==> góc BAD= goc ADB
-> tam giac BAD cân tại B
b) xet tam giac ADH và tam giac ADE ta có
AD= AD ( cạnh chung)
goc HAD = goc DAC ( AD là p/g goc HAC)
goc AID = góc AIE (=90)
--> tam giac ADH= tam giac ADE (g-c-g)
-< AH= AE ( 2 canh tương ứng)
Xét tam giac AHD và tam giac AED ta có
AD=AD ( cạnh chung)
AH=AE (cmt)
goc DAH= goc DAE ( AD là p/g HAC)
-> tam giac AHD= tam giac AED ( c-g-c)
-> goc AHD= goc AED ( 2 góc tương ứng
mà góc AHD = 90 ( AH vuông góc BC)
nên AED =90
-> DE vuông góc AC
c) Xét tam giac ABH vuông tại H ta có
AB2= AH2+BH2 ( dly pi ta go)
152=122+BH2
BH2 =152-122=81
BH=9
ta có BA=BD ( tam giác ABD cân tại B)
BA=15 cm (gt)
-> BD=15
mà BH+HD=BD ( H thuộc BD)
nên 9+HD=15
HD=15-9=6
Xét tam giác ADH vuông tại H ta có
AD2=AH2+HD2 ( định lý pitago)
AD2=122+62=180
-> AD=\(\sqrt{180}=6\sqrt{5}\)
a) Vì BD = BA nên ΔΔBAD cân tại B
=> BADˆBAD^góc BAD = g BDA (góc đáy) →→-> đpcm
b) Ta có: góc BAD + g DAC = 90o
=> g DAC = 90o - g BAD (1)
Áp dụng tc tam giác vuông ta có:
g HAD + g BDA = 90o
=> g HAD = 90o - g BDA (2)
mà góc BAD = g BDA (câu a)
=> gDAC = g HAD
=> AD là tia pg của g HAC.
c) Áp dụng tc tổng 3 góc trong 1 tg ta có:
g AHD + g HDA + g HAD = 180o
=> 90o + g HDA + g HAD = 180o
=> g HDA + g HAD = 90o (3)
g DAC + g DKA + g ADK = 180o
=> g DAC + 90o + g ADK = 180o
=> g DAC + g ADK = 90o (4)
mà gDAC = g HAD hay gDAK = gHAD
Xét tgHAD và tgKAD có:
g HDA = g ADK (c/m trên)
AD chung
g HAD = g DAK (c/m trên)
=> tgHAD = tgKAD (g.c.g)
=> AH = AK (2 cạnh t/ư)