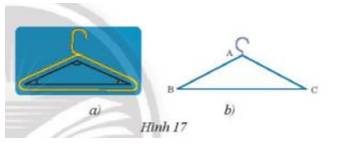
Phần thân của một móc treo quần áo có dạng hình tam giác cân (Hình 17a) được vẽ lại như Hình 17b. Cho biết AB = 20 cm; BC = 28 cm và \(\widehat B\)= 35°. Tìm số đo các góc còn lại và chu vi của tam giác ABC.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HQ
Hà Quang Minh
Giáo viên
8 tháng 9 2023
Áp dụng định lý Pythagore vào tam giác vuông \(ADE\) ta có:
\(D{E^2} + A{E^2} = A{D^2}\)
\(D{E^2} = A{D^2} - A{E^2} = {61^2} - {60^2} = 121 = {11^2}\)
\(DE = 11\) (cm)
Độ dài \(AB\) là: \(92 - 11.2 = 70\) (cm)
21 tháng 10 2021
Chu vi hình thang cân là:
15 + 25 + 7. 2 = 54 (cm)
Độ dài phần còn lại làm móc treo là:
60 – 54 = 6 (cm)
Vậy phần còn lại làm móc treo có độ dài 6cm.
HT
24 tháng 12 2021
Đáp án:
tam giác : ADC =60 tam giác : ABD=300 (cm2)
50/100
Giải thích các bước giải:
Diện tích của hình thang ABCD là :
( 20+40) x 30:2=900(cm2)
Diện tích hình tam giác ADC là :
40x 30:2 =600 (cm2)
Diện tích hình tam giác ABD là :
900-600=300 (cm2)
Tỉ số phần trăm của hai tam giác ADC và ABD là:
300:600= 50/100
Đáp số : tam giác : ADC =600 (cm2)
: tam giác : ABD=300 (cm2)
50/100
Vì tam giác ABC cân tại A
\( \Rightarrow \) AB = AC = 20 cm
\( \Rightarrow \) Chu vi tam giác ABC = AB + AC + BC = 20 + 20 + 28 = 68 cm
Vì \(\Delta ABC \) cân tại A \( \Rightarrow \widehat B = \widehat C\) = 35°
Mà tổng 3 góc trong một tam giác là 180°
\( \Rightarrow \widehat A = {180^o} - \widehat B - \widehat C = {180^o} - {35^o} - {35^o} = {110^o}\)