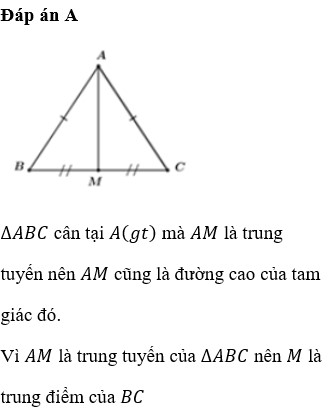
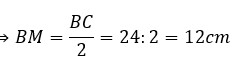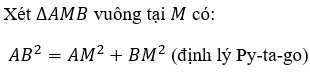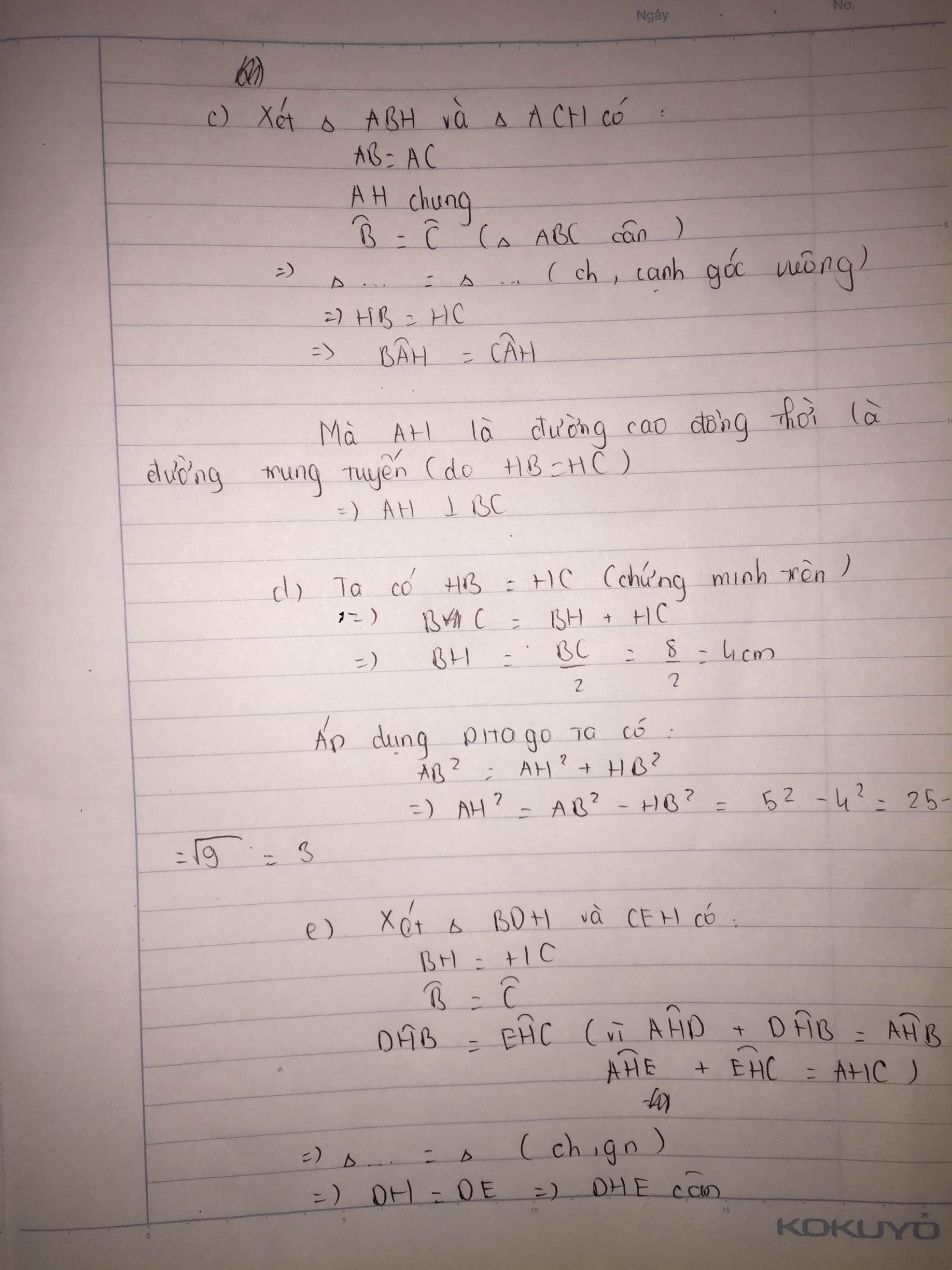Cho tam giác ABC cân tại A, AB = AC =5 cm; BC =8 cm. Kẻ AH vuông góc với BC (H thuộc BC)
a) Chứng minh HB = HC.
b) Tính AH.
c) Kẻ HD vuông góc với AB (D thuộc AB); HE vuông góc với AC (E thuộc AC). Chứng minh: tam giác HDE là tam giác cân.
d) Chứng minh: DE // BC.