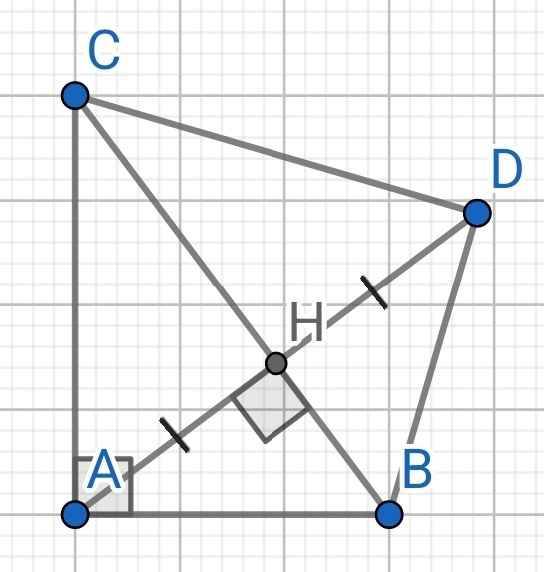
Cho tam giác BCD vuông tại B. BC=15 ; BD=20. BH vuông góc vs CD.
- Tính độ dài các đoạn thẳng CD,CH
- Gọi A là điểm sao cho tứ giác ABCD là hình thang cân có đáy là các cạnh AB;CD.Tính diện tích hình thang ABCD.
- Giải giúp mk nha .Đúng mk tick cho
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
13 tháng 1 2021
a) Ta có: AD=AC(gt)
mà A nằm giữa hai điểm C và D(gt)
nên A là trung điểm của CD
Xét ΔBCD có
BA là đường trung tuyến ứng với cạnh CD(A là trung điểm của CD_
BA là đường cao ứng với cạnh CD(BA⊥CA, D∈CA)
Do đó: ΔBCD cân tại B(Định lí tam giác cân)
TG
13 tháng 1 2021
Sửa đề: Góc B = 30 độ
----------------------------------------
a) Ta có: \(\widehat{BAC}+\widehat{BAD}=180^0\) (kề bù)
\(\Rightarrow\widehat{BAD}=180^0-\widehat{BAC}=180^0-90^0=90^0\)
Xét ΔBAD và ΔBAC ta có:
AD = AC (GT)
Góc BAD = Góc BAC (= 900)
AB: canhj chung
=> ΔBAD = ΔBAC (c - g - c)
=> Góc C = Góc D (2 góc tương ứng)
=> Tam giác BDC cân tại B (1)
ΔABC vuông tại A
\(\Rightarrow\widehat{ABC}+\widehat{C}=90^0\)
\(\Rightarrow\widehat{C}=90^0-\widehat{ABC}=90^0-30^0=60^0\left(2\right)\)
Từ (1) và (2) => Tam giác BDC đều
b) Tam giác BDC đều
=> BC = CD
Mà: CD = 2. AC
=> BC = 2.AC
26 tháng 1 2022
a: Xét ΔCBA vuông tại B và ΔCHA vuông tại H có
CA chung
\(\widehat{BCA}=\widehat{HCA}\)
Do đó: ΔCBA=ΔCHA
Suy ra: BA=HA
b: Xét ΔBAE vuông tại B và ΔHAD vuông tại H có
BA=HA
\(\widehat{BAE}=\widehat{HAD}\)
Do đó: ΔBAE=ΔHAD
CM
17 tháng 3 2017
a) Chứng minh được tam giác ABC = tam giác A.BD (c-g-c), từ đó suy ra được tam giác BCD đều
b) Dùng kết quả câu a, ta có BC = CD = 2AC
21 tháng 3 2021
a) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(AB^2+AC^2=BC^2\)
\(\Leftrightarrow AC^2=BC^2-AB^2=15^2-9^2=144\)
hay AC=12(cm)
Vậy: AC=12cm
KV
11 tháng 11 2023
a) Xét hai tam giác vuông: ∆ABH và ∆DBH có:
AH = DH (gt)
BH là cạnh chung
⇒ ∆ABH = ∆DBH (hai cạnh góc vuông)
b) Sửa đề: Chứng minh ∠BDC = 90⁰
Do ∆ABH = ∆DBH (cmt)
⇒ ∠ABH = ∠DBH (hai góc tương ứng)
AB = BD (hai cạnh tương ứng)
Do ∠ABH = ∠DBH (cmt)
⇒ ∠ABC = ∠DBC
Xét ∆ABC và ∆DBC có:
AB = BD (cmt)
∠ABC = ∠DBC (cmt)
BC là cạnh chung
⇒ ∆ABC = ∆DBC (c-g-c)
⇒ ∠BAC = ∠BDC = 90⁰
Vậy ∠BDC = 90⁰
Theo định lý pytago =>DC=\(\sqrt{CB^2+DB^2}\)=\(\sqrt{15^2+20^2}\)=25
\(\widehat{HBD}\)+ \(\widehat{D}\)=900 \(\widehat{C}\)+\(\widehat{D}\)=900 => \(\widehat{C}\)=\(\widehat{HBD}\) =>\(\Delta\)HBD~\(\Delta\)BCD(gg)
=>\(\frac{HB}{BC}\)=\(\frac{HD}{BD}\)<=> \(\frac{HB}{15}\)=\(\frac{HD}{20}\)(1) Mặt khác: BC*BD=CD*BH=>BH=15*20/25=12
Thay vào (1) =>HD=12/15 *20=16 =>HC =9
ABCD là hình thang cân=> BH cũng chính là đường cao của hình thang
Đáy nhỏ AB dài là: 25 - 9 - 9 =7
Diện tích hình thang ABCD là:(7+25)*12/2=192(dvdt)