3:

góc C=90-50=40 độ

Xét ΔABC vuông tại A có sin C=AB/BC

=>4/BC=sin40

=>\(BC\simeq6,22\left(cm\right)\)

\(AC=\sqrt{BC^2-AB^2}\simeq4,76\left(cm\right)\)

1:

góc C=90-60=30 độ

Xét ΔABC vuông tại A có

sin B=AC/BC

=>3/BC=sin60

=>\(BC=\dfrac{3}{sin60}=2\sqrt{3}\left(cm\right)\)

=>\(AB=\dfrac{2\sqrt{3}}{2}=\sqrt{3}\left(cm\right)\)

còn câu 2 

\(\dfrac{AB}{AC}=\dfrac{3}{4}\Rightarrow AB=\dfrac{3}{4}AC\)

Áp dụng hệ thức lượng:

\(\dfrac{1}{AH^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}\Leftrightarrow\dfrac{1}{12^2}=\dfrac{1}{\left(\dfrac{3}{4}AC\right)^2}+\dfrac{1}{AC^2}\)

\(\Rightarrow AC^2=400\Rightarrow AC=20\)

\(AB=\dfrac{3}{4}AC=15\)

\(BC=\sqrt{AB^2+AC^2}=25\)

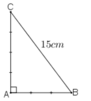
sai đề, sửa: BC=15cm 

\(\frac{AB}{AC}=\frac{3}{4}\Rightarrow AB=\frac{3AC}{4}\)

Áp dụng định lý pytago vào tam giác vuông ABC. ta có:

AB²+AC²=BC²

=> \(\left(\frac{3}{4}AC\right)^2+AC^2=15^2\)

\(AC^2.\left(\frac{9}{16}+1\right)=15^2\Rightarrow AC^2.\left(\frac{5}{4}\right)^2=15^2\)

\(\Rightarrow AC^2=15^2.\left(\frac{4}{5}\right)^2=12^2\Rightarrow AC=12\)

\(AB=\frac{3.AC}{4}=9\)

-bài này vẽ hình làm cảnh à :V

Theo đề bài ta có:

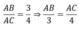
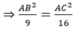
Theo tính chất dãy tỉ số bằng mhau ta có:

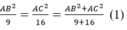
tam giác ABC vuông tại A

Áp dụng định lí pitago vào tam giác ABC ta có:

BC2 = AB2 + AC2 (2)

Từ (1) và (2) suy ra:

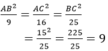
AB2 = 9. 9 = 81 ⇒ AB = 9 cm (vì AB > 0)

AC2 = 16. 9 = 144 ⇒ AC = 12 cm (vì AC > 0)

Ta có:tam giác ABC có góc A=90 độ

=>Tam giác ABC vuông tại A.    

Ta có:AB/AC=3/4   =>AB/3=AC/4

ÁP DỤNG T/C DÃY TỈ SỐ BĂNG NHAU.TA CÓ

AB/3=AC/4=AB²+AC²/3²+4²=15²/9+16=225/25=9

=>AB=

=>AC=

Bạn hãy tính đi nhé 

 Gọi D là điểm thỏa mãn tứ giác ABDC là hình chữ nhật.

Ta có

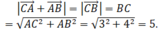
Chọn C