Cho hình chữ nhật ABCD có AD=8cm; CD=15cm
a)Tính AC
b) Đường thẳng qua D và vuông góc với AC tại M cắt AB ở N và cắt tia CB ở I, Tính MD
c)C/m: MD^2=MN.MI
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CD
1
QT
1
10 tháng 10 2023
Tham khảo:
Hình chữ nhật ABCD có AB và AD vuông góc với nhau tại A.
- Vẽ đoạn thẳng AB = 5 cm và đoạn thẳng AD = 8 cm vuông góc với nhau tại A.
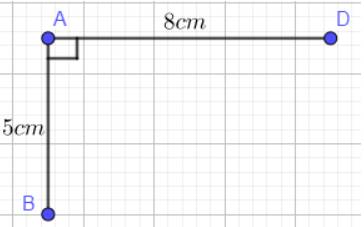
- Qua B vẽ đường thẳng b vuông góc với AB.
- Qua D vẽ đường thẳng d vuông góc với AD.
Hai đường thẳng b và d cắt nhau ở C.
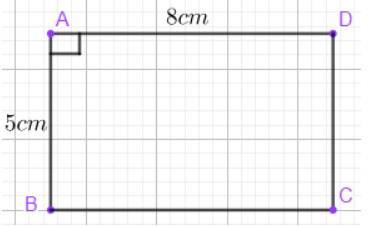
Ta được ABCD là hình chữ nhật cần vẽ.
10 tháng 3 2023
a: \(BD=\sqrt{8^2+6^2}=10\left(cm\right)\)
b: Xét ΔDHA vuôg tại H và ΔDAB vuông tại A có
góc HDA chung
=>ΔDHA đồng dạng với ΔDAB
c: ΔDHA đồng dạng với ΔDAB
=>DH/DA=DA/DB
=>DA^2=DH*DB
CM
25 tháng 3 2019
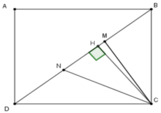
Ta có CD = AB = 9cm; BC = AD = 8cm nên SBCD = 1 2 BC.DC = 1 2 .8.9 = 36cm2
Kẻ CH ⊥ BD tại H
Ta có: SBCD = 1 2 CH.BD; SCMN = 1 2 CH.MN mà MN = 1 3 BD
=> SCMN = 1 3 SBCD = 1 3 .36 = 12cm2
Đáp án cần chọn là: A
a: Xét ΔADC vuông tại D có
\(AC^2=AD^2+DC^2\)
hay AC=17(cm)