Cho tam giác MNP vuông tại M (MN>MP).; D là điểm trên NP. Qua D kẻ Dx vuông góc NP và cắt mn tại E, cắt PM tại F. Chứng minh rằng:
a) tam giác MNP đồng dạng tam giác DFP
b) NE.MN=ND.NP
c)NE.MN + PE.PI không phụ thuộc vào vị trí điểm D ( I là giao điểm của NE và NP)
d) Tìm vị trí của D trên NP sao cho \(\dfrac{PD}{PN}=\dfrac{PM}{PF}\)

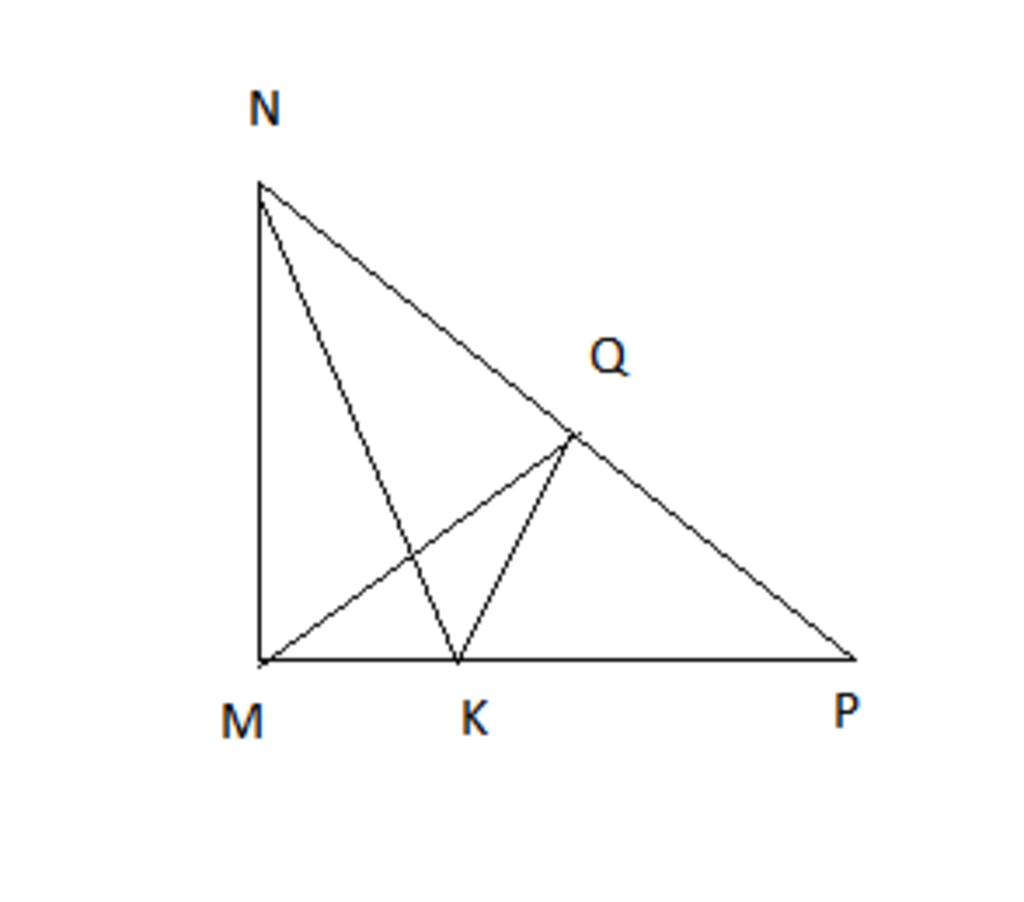
câu a
xét tam giác mnp và tam giác dfp có
góc nmp = góc fdp (=90 độ)
chung góc p
=> tam giác mnp đồng dạng tam giác dfp (gg)
câu b
xét tam giác mnp và tam giác dne có
góc nmp = góc nde (=90 độ)
chung góc n
=> tam giác mnp đồng dạng tam giác dne (gg)
=> \(\dfrac{ne}{np}=\dfrac{dn}{mn}\)
=> ne . mn = nd . np
(lưu ý: hình vẽ chỉ mang tính chất minh hoạ :) )
chúc may mắn, 2 câu còn lại để mình xem, lâu ko làm lại dạng này