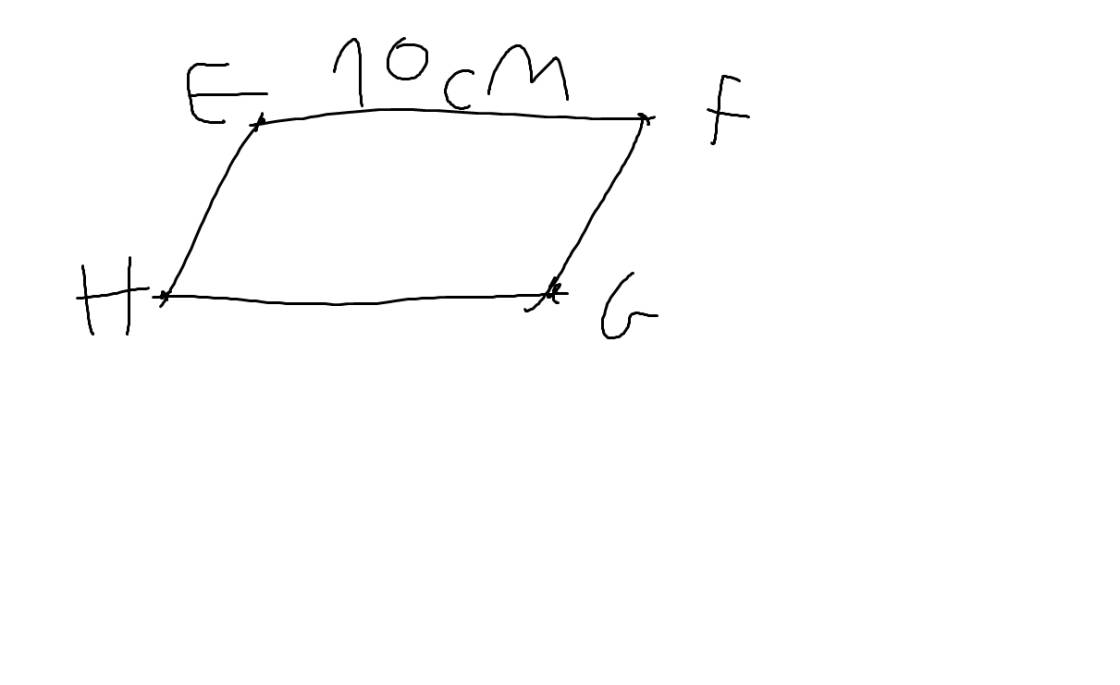
2:

\(GH=\dfrac{1}{2}EG=\dfrac{1}{2}\cdot10=5\left(cm\right)\)

Chu vi hình bình hành là:

\(2\cdot\left(10+5\right)=2\cdot15=30\left(cm\right)\)

1:

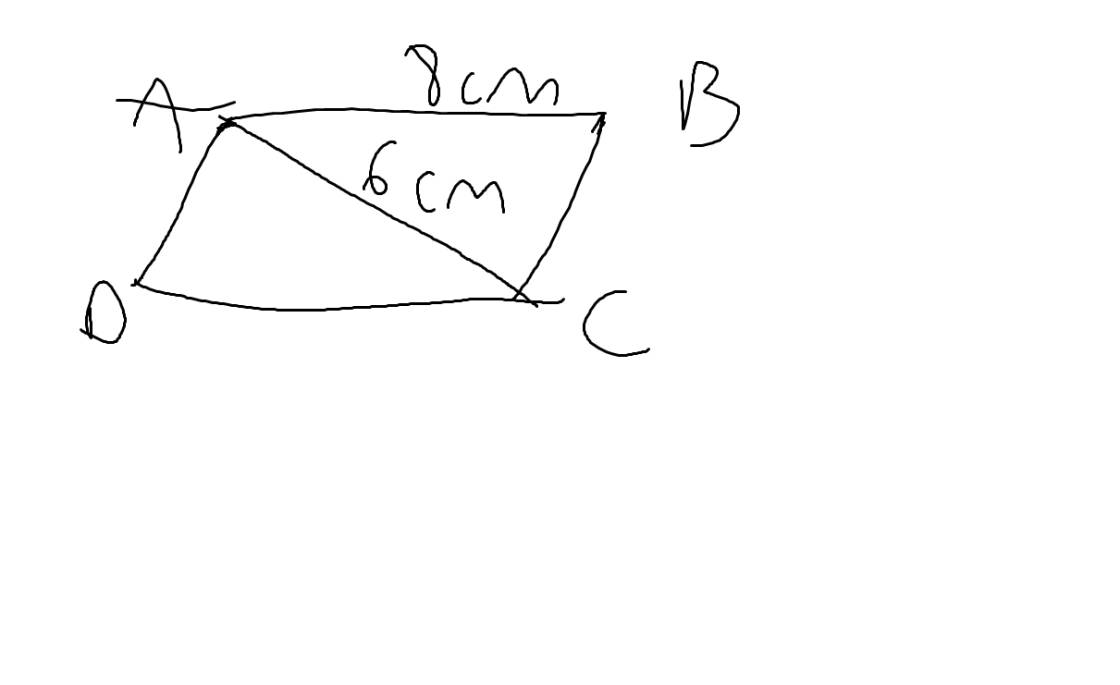
Diện tích hình thoi ABCD hay diện tích hình bình hành MNPQ là:

18 x 16 : 2 = 144 (cm²)

Chiều cao của hình bình hành MNPQ là:

144 : 9 = 16 (cm)

Đáp số: 16 cm

Thanks bạn!

a: S CAB=1/2*CM*AB

S CAD=1/2*CN*AD

mà ΔCAB=ΔCAD

nên CM*AB=CN*AD

b: Xét ΔAID vuông tại I và ΔANC vuông tại N có

góc IAD chung

=>ΔAID đồng dạng với ΔANC

=>AI/AN=AD/AC

=>AI*AC=AN*AD

Xét ΔHCB vuông tại H và ΔNAC vuông tại N có

góc HCB=góc NAC

=>ΔHCB đồng dạng với ΔNAC

=>HC/NA=CB/AC

=>CB*NA=HC*AC=AD*AN

=>AD*AN+AB*AM=AC^2

Chu vi hình bình hành là:

 2(15+8)=46 cm

  Đ/s: 46cm

Chu vi hình bình hành là :                                                                                                                                                                     ( 15 + 8 ) x 2 = 46 ( cm )                                                                                                                                                                                      Đ/S : 46 cm                                                                                                                                                                              tk mình nha

Chu vi hình bình hành ABCD là: 

\(\left(12+8\right)\times2=40\left(cm\right)\)

Diện tích hình bình hành ABCD là: 

\(12\times6=72\left(cm^2\right)\)

                                                          Giải

Chu vi hình bình hành ABCD đó là :

\(\left(12+8\right)\times2=40\) ( cm )

Diện tích hình bình hành ABCD đó là :
\(12\times6=72\)( cm² )

              Đáp số : Chu vi : \(40\)cm ; Diện tích : \(72\)cm²

Vì hình ABCD là hình bình hành nên cạnh AD = BC = 3cm. Vì hình BMNC là hình thoi nên có các cạnh bằng nhau, do đó ta có :

         BC = BM = MN = 3 cm

Chiều cao tương ứng cạnh DC của hình bình hành ABCD là :

         8 : 4 = 2 (cm)

Chiều cao tương ứng cạnh DC cũng là chiều cao tương ứng cạnh NC do đó diện tích hình thoi BMNC là :

         3 x 2 = 6 (cm2) 

            Đáp số : 6 cm2

Chu vi hình bình hành là: \(\left(12+8\right)\times2=40\)(cm)

Diện tích hình bình hành là: \(\left(12+8\right)\times6=60\)(cm^2)

Xét ΔAHB vuông tại H và ΔAMC vuông tại M có

góc HAB chung

=>ΔAHB đồng dạng với ΔAMC

=>AH/AM=AB/AC

=>AB*AM=AH*AC

Xét ΔHCB vuông tại H và ΔNAC vuông tại N có

góc HCB=góc NAC

=>ΔHCB đồng dạng với ΔNAC

=>CB/AC=HC/NA

=>CB*NA=HC*AC=AD*AN

=>AD*AN+AB*AM=AC^2